| Columns Retired Columns & Blogs |
Excellent time-trip down memory lane. I was hooked on CD in 1988.
I became hooked on SACD in 2001.
Following hard on the heels of Peter van Willenswaard's report in the May issue that the Dutch company Philips had developed a 1-bit D/A converter that offered 16-bit resolution, called the "Bit Streamer," I visited both Philips' research laboratories (footnote 9) in Eindhoven, Holland, and their CD-player factory in Hasselt, Belgium, and was given more details about this system.
The disadvantage inherent to a conventional multi-bit linear D/A system is these days well-known: errors in the relationship between the currents switched by the individual bits, particularly the Most Significant Bit (MSB), lead to a non-linear transfer function (fig.1), which manifests itself as level errors and added distortion which can become significant at low levels and high frequencies. Nearly all high-end players, apart from those using the Philips 16-bit, 4x-oversampling chip set, feature some kind of linearity adjustment, therefore, either in the manufacturing stage, where lasers are used to trim on-chip resistors to the precise value, or in the assembly, where trimpots allow individual bit currents to be adjusted for lowest overall distortion. (The Burr-Brown 18-bit DAC, for example, featured in the Onkyo DX-G10 and California Audio Labs Tempest SE, has trimpots for its four MSB currents.)
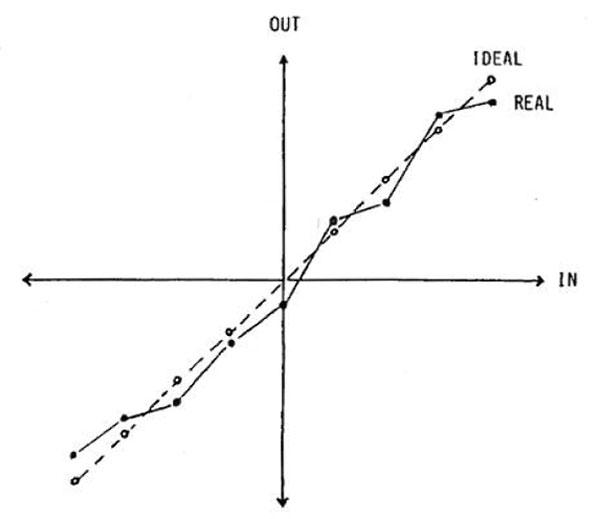
The disadvantage of such calibration procedures, however, is that they may only produce optimum performance either for a small length of time or under identical conditions of temperature, etc., as when the original calibration was carried out. (Use a laser to modify a resistor's value and it is possible that you will heat it up as you do so, resulting in a further unwanted change when it cools down again.)
The 16-bit Philips system avoids the need for such calibration as the current sources for the most significant bits are time-averaged—see my review of the LHH1000 CD player for a more detailed explanation of this "Dynamic Element Matching"—but the user is then stuck, therefore, with the DAC's intrinsic linearity, which is why Philips grades their chips. But whatever the particular topology used, I am sure that many audiophiles will agree that CD players using state-of-the-art DACs can achieve very high levels of performance, sounding almost as good as can be expected from the CD medium. However, the very complexity of the task suggests that there should be a simpler, more elegant way to achieve the same result, a DAC technique which is inherently linear without adjustment.
Such is said to be the case with Philips' Bit-Streamer topology. Rather than use the obvious and so-far ubiquitous technique where voltage or current are divided according to the digital word input, and having to accept the real-world errors that occur in such analog quantity division, why not change the system so that you are now dividing something where standard techniques have proved to have a considerably greater degree of inherent accuracy: time. Any electronic engineering student will tell you that dividing a pulse train with a period of 1/2T into a half-speed one of period 1/T with astonishingly high accuracy is about the simplest thing to do compared with dividing a reference voltage or current into two identical halves to the same accuracy. In addition, any errors inherent in the operation of the 1-bit DAC are said to result, not in non-linearity, but, as shown in fig.2, in an amplitude gain error and/or a DC offset, both benign and easily compensated for.
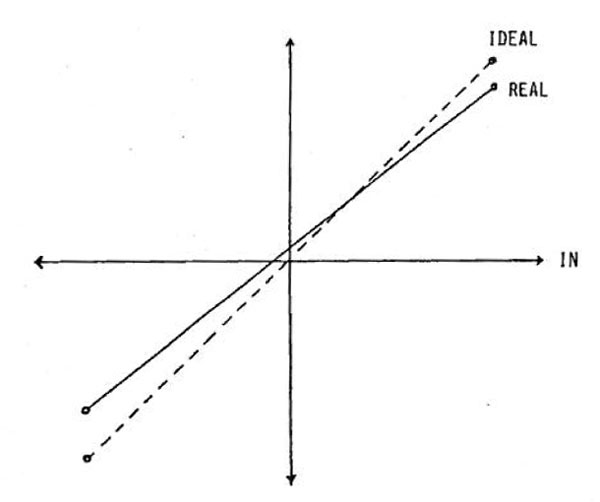
Fig.3 shows a block diagram for a D/A process using Philips' 44-pin SAA7320 CMOS Bit-Streamer chip, which was prototyped at the Mullard MOS plant in Southampton, England, but will be produced in quantity by Valvo in Hamburg, West Germany. (Both plants are wholly owned subsidiaries of Philips.) Apparently everything in the block diagram, from input digital filter to output analog filter (capacitors and timing crystal excepted), is realized on the one piece of silicon. A standard, time-multiplexed, error-corrected, 44.1kHz-sampled stream of 16-bit stereo data retrieved from a CD is fed to a 4x-oversampling Finite Impulse Response (FIR) digital filter. This uses 12-bit coefficients and 28-bit internal words, rounded off in two stages to 16, and outputs a 176kHz stream of multiplexed 16-bit data, which feeds separate left and right 32x-oversampling stages.
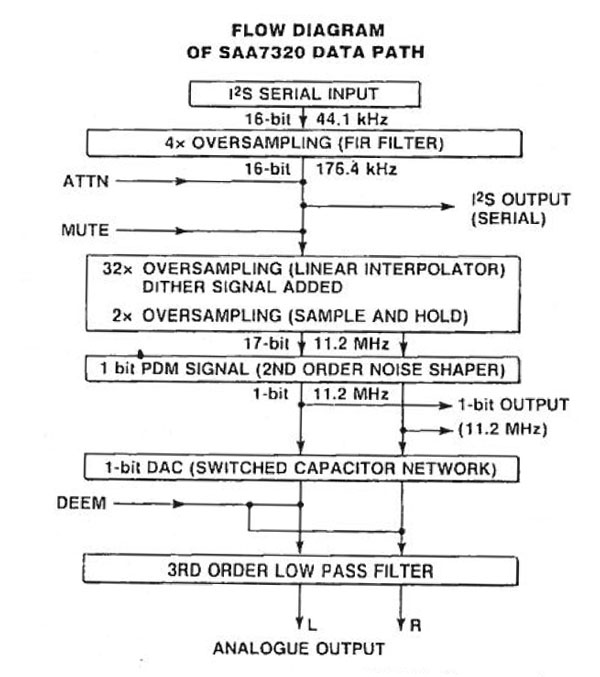
Rather than repeat the original samples or insert zeroes to achieve the new sampling rate, the 32x-oversampler interpolates between adjacent samples to generate new data, and digital dither (–20dB at 352kHz) is added at this stage to minimize requantizing distortion and avoid idling patterns in the following noise shaper which, it is said, could lead to non-linearity. A sample-and-hold circuit increases the effective sampling rate by an additional factor of two (but without interpolation). The output from this stage consists of 17-bit data (the dither adds one bit) at a 256x rate, ie, at 11.2896MHz. This is where something akin to magic occurs.
A second-order noise shaper or code converter, operating with 21-bit internal words, takes in the 17-bit data and outputs equivalent 1-bit data at the same rate. When these oversampled, noise-shaped 1-bit data are D/A-converted and time-averaged by the final third-order–Butterworth, low-pass filter, the original 16-bit resolution of the CD data is said to have been preserved.
This is hard to believe. Let me expand, following an example given by Jos Timmermans of the Philips CD-player facility: Imagine you have a first-order noise shaper, the 1-bit output of which can either take on a value of "1" or "0." At the input of the noise shaper is an adder circuit which computes the sum of the input value and the remainder left over when the previous output was truncated to one bit. Imagine that the input to this circuit is a digital word representing 0.25, oversampled without interpolation at a 4x rate; ie, the input consists of four words representing 0.25, 0.25, 0.25, and 0.25. The first output bit will be a "0" (0.25 is nearer to 0 than it is to 1); the remainder of +0.25 is fed back to the circuit's input. The second output will also be a "0," as the input of 0.25 plus the remainder from the previous bit of +0.25 equals 0.5. (I have arbitrarily assumed that 0.5 will be decoded as a 0 rather than a 1.) The remainder is now +0.5, which in turn is fed to the input to be added to the next value to give 0.75. Now the output from the circuit will be a 1, with a remainder of –0.25, which when fed back to be added to the fourth sample, gives 0, of course. The final bit output from the noise shaper is therefore a 0, resulting in the 1-bit output stream consisting of "0010," which when time-averaged by the final low-pass filter (which will not pass the 4x-oversampling frequency), will give an analog value of 1 divided by 4; ie, 0.25.
I'll leave it to you to determine that for a 4x-oversampled input signal equivalent to the analog value 0.75, the 1-bit datastream output by the device will be "1011," which, when time-averaged, will be equal to 0.75 (but note that the noise shaper in this example has to have a higher internal dynamic range than the input signal would seem to require).
In effect, the use of a first-order noise shaper can be seen to give a resolution of two extra bits in the word length at the expense of quadrupling the necessary data rate—in the above example, the 1-bit output is arranged to carry four times as much information as it would intuitively seem to be able to. This is why the original Philips SAA7030 digital filter chip, which incorporated a similar first-order noise shaper, was able to wrest 16-bit resolution from the 14-bit TDA1540 DAC. (Note that while Philips' current SAA7220 digital filter may run at a 4x rate, thus relaxing the analog postfilter requirements, it doesn't have a noise shaper and therefore doesn't offer more than 16-bit resolution. Mere oversampling in itself, I believe, does not increase intrinsic resolving power, whether it be 4x, 8x, or 16x (footnote 10).
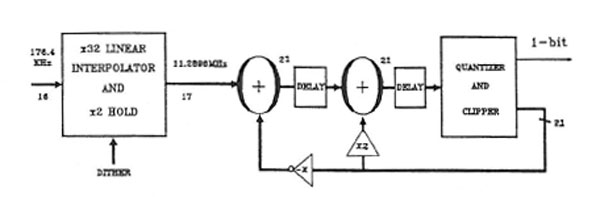
A second-order noise filter in effect has two separate "feedback" loops for the remainder left over after truncation, and thus is considerably more complex. It offers a considerably greater increase in resolving power, however: from the figures given by Philips, it would seem that the configuration used in the SAA7320 (see fig.4, where twice the remainder is added at one point and the inverse of the remainder at another), in conjunction with the interpolation and digital dither employed, does enable the 1-bit DAC to achieve full 16-bit resolution. The necessary tradeoff, of course, is the need to resample the data at 11.2896MHz, something that Mr. Timmermans said was not possible to implement in monolithic silicon until relatively recently. Why not go beyond a second-order noise shaper, thus increasing resolution even further? As I understand it, third-order and above noise shapers are inherently unstable, though I am told that it is possible to arrange for one to be metastable; ie, arrange for it to avoid the regions where it goes crazy—or add an ALT-CTRL-DEL button.
I would imagine that if you low-pass-filter this 1-bit, 11.3MHz datastream, which represents the information in a pulse-width-modulated form, then you would recover the analog signal. However, I believe that Philips was forced to think of a new technique for the final D/A conversion due to the fact that PWM techniques have been heavily patented by the Japanese. As can be seen from fig.3, the 1-bit datastream is fed to a 1-bit DAC which consists of an on-chip switched-capacitor network. This outputs a stream of bipolar pulses, going from the middle of the voltage window to either the positive rail or the negative rail. As can be seen in fig.5 (which is simulated), this process represents the original analog waveform in a Pulse-Density-Modulated form. Fig.6 shows a typical spectrum for an 11.3MHz PDM-encoded 2kHz tone; when this PDM signal is low-pass filtered—and preventing that RF hash from corrupting other circuits inside the box will not be a trivial task—then all you will be left with is the original analog signal.

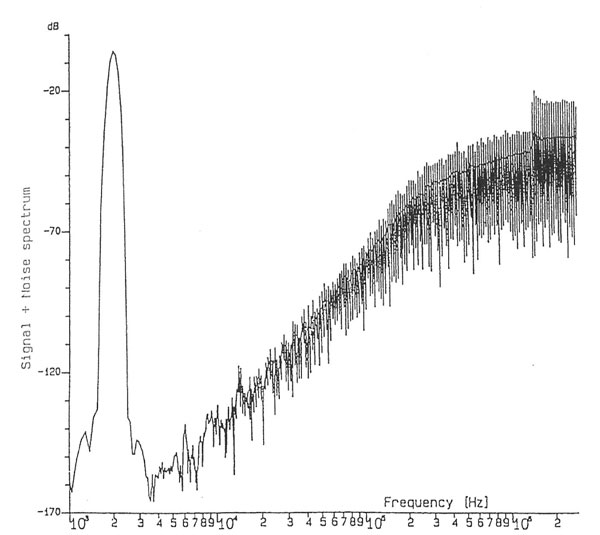
Like I said: magic.
According to the chip pinout, all inputs and outputs for the on-chip op-amps used for the final low-pass filtering, as well as the left and right DAC/integrator outputs, are made available, which facilitates getting even higher performance from the SAA7320. Two can be used: one fed the conventional datastream, the other with the same data with reversed polarity. The two left outputs, mirror images of each other, can then be taken to the inputs of a differential amp on one chip, then to the low-pass filter on the same chip, the two rights to a differential amp, then to a low-pass filter on the other chip. The differential operation should minimize gain and DC errors, while separating the left and right analog channels on individual chips will maximize separation.
As stated earlier, the figures for the SAA7320—96dB dynamic range, S/N+THD better than –90dB, passband ripple of less than 0.035dB, and stop-band attenuation of 60dB—indicate true 16-bit resolution, which, coupled with the 1-bit converter's inherent linearity, would suggest its use in high-end players. Philips even reports that initial listening tests show the system to sound at least as good as their current 16-bit system. But therein lies a question: with the Bit Streamer chip in production, why, then, is Philips sticking with its conventional 16-bit chip set for its own models and so far appearing only to offer the SAA7320 as an OEM DAC to, for example, Japanese companies? I was unable to get an answer to that question, other than a statement from Mr. Timmermans that at present the Bit Streamer DAC is more expensive than even the top-selected TDA1541A 16-bit DAC/SAA7220B digital filter combination, but I can say that Philips seems to be preparing to use the technology in a wealth of future electronic components.
In development is a reduced-performance version of the 7320, the 7340, which will also incorporate the demodulation, error-correction, and concealment functions at present implemented in either the SAA7210 or SAA7310 chips. In effect, the entire digital and analog circuits of a CD player, following the RF preamplifier that processes the signal from the pickup, can be contained on two chips, one 80-pin 7340, and one 8k RAM IC. Farther along down the line is a dual-chip bit-stream set, the PCF5022 and '23, which will function as the core of an all-digital preamplifier/decoder. Digital inputs will be processed directly, while analog inputs will first be converted to digital by a bit-streamer A/D converter incorporated in the 5023 chip. (Interestingly for surround-sound enthusiasts, this set has four DACs.)
A system based on this chip set will, of course, use analog power amplifiers, but Philips Research Laboratories, I was told, have developed a number of loudspeakers that will operate directly on a digital input signal. Discussion of these, however, was left for the future.—John Atkinson
Footnote 10: If you laboriously work it through with pencil and paper, you can show that the first-order noise shaper described above gives an increase in resolution proportional to the degree of oversampling. Thus, 8x-oversampling will enable a first-order noise shaper with a 1-bit output stage to resolve levels down to 1/8 of the 1-bit quantizing step—ie, an increase in resolution of 3 bits—and 16x-oversampling will result in a 4-bit increase. But note that it is the noise shaper in combination with the oversampling which achieves the increase in resolution, not the oversampling on its own.

Excellent time-trip down memory lane. I was hooked on CD in 1988.
I became hooked on SACD in 2001.

Thank you for posting this! Love reading about the old stuff.
Out of curiosity, has Stereophile ever done a review of an Elcaset deck? Saw an article about it on another site and now I'm curious if you guys ever measured one.

... is a much-modified Philips CD-60 (built early 1990).
it uses a TDA1541A (double crown) / SAA7220/B combo noted in this article.
No way have I heard the best digital playback gear avail today (mid. 2017).
I'm sure the latest Meridian, PS Audio or Chord DACs will provide v. good sound.
I have heard (and/or own) some Musical Fidelity DACs from a few years ago.
Also have the DiyParadise TDA1545A-based non-oversampling Monica DAC.
My modded CD-60 easily beats those.And, in some ways, also surpasses my VPI-HW19/Rega RB300/Sumiko BP Special analog rig.
I think Philips SENSIBLY used their R/D funds and facilities when they came up with those now-classic digital ICs.
IMPLEMENTATION is very important. So even the poor-sounding Bitstream/MASH DACs could sound okay if the PSU was decent and the output section was discrete.