| Columns Retired Columns & Blogs |
Jitter, Bits, & Sound Quality
Jitter is not what digital sound quality induces in the listener; rather it is the instability in the clock signal that controls exactly when the analog waveform is sampled in the original A/D conversion, or when the digital word input into a DAC results in an analog voltage being produced at the chip's output. "So what?" is the response of digital advocates, "As long as a digital one is recognized as a one and a digital zero as a zero, then how can there be any difference in sound?" goes their argument, normally culminating in a fervently expressed "Bits is bits!"
Footnote 1: In Stereophile Vol.9 No.2, March 1986, where he said in his interview with J. Gordon Holt (p.110) that "One least significant bit of amplitude is equivalent to 200 picoseconds of time...if the timing is off, the output...will not correspond in amplitude to the digital code."—John Atkinson
Would that things were that simple. As my violin teacher used to say, "The right note in the wrong place is the wrong note." It's the same with digital data. Uncertainty in the precise timing of that digital one or zero results in a loss of system resolution, with audible effects on the finally recovered analog signal. In November's "Industry Update" (Vol.13 No.11, p.78, see Sidebar), Stereophile's Dutch correspondent Peter van Willenswaard neatly showed how an uncertainty of well below 1ns—one billionth of a second!—in the timing accuracy of a 16-bit digital datastream resulting from an original analog signal sampled every 22.7µs, a time interval nearly 23 thousand times larger, equated with a loss of one bit's worth of resolution.
As Meridian's Bob Stuart was the first engineer I had ever read who discussed the effect of digital data jitter (footnote 1), and had explained to me at the 1990 WCES that one of the factors behind the sound quality of the Meridian 208 CD player that I review elsewhere in this issue was not so much its use of Bitstream technology but a much-improved transport and data-recovery electronics, I thought it worth looking further at the subject of jitter.
In a recent issue of the Journal of the Audio Engineering Society, Steven Harris of Crystal Semiconductor looked at the effect of timing jitter on A/D converters (footnote 2). Included in his paper was a Basic program for simulating the effect of any amount or kind of timing jitter on any frequency or level of sinewave signal with A/D converters running with any bit resolution at any sampling frequency (footnote 3). The program outputs a data file consisting of the integer numbers representing the digitized sinewave; with a 16-bit system these range from -32,768 to +32,768. It was a moment's work to write a couple of extra program lines so that these time-data files could be imported by FFT analaysis software. I could therefore synthesize the action of jitter on a digitized waveform and examine the resultant analog effects.
(The Harris program is specifically intended for A/D converters, where not-totally-synchronous sampling produces data which are then read with a highly precise clock—something that is easy to synthesize. The situation with a CD player's DACs, where nominally highly precisely clocked data are decoded with a degree of time uncertainty in the sample timing, is clearly the mirror image. The implications of these simulations will clearly, therefore, be transportable to DACs.)
I set up the parameters for a 16-bit ADC sampling at 44,100Hz—the CD standard—and synthesized a series of unfortunate 10kHz sinewaves afflicted with jitter ranging from none to 2ns peak-peak (ie, the exact sample time can vary by +1ns or -1ns), with the jitter either random (white) noise or a 1kHz sinewave. I chose 1kHz, not because it is typical of the kind of frequency a jitter signal might have, but because it represents a readily identifiable spurious signal. Jitter of 1ns is typical of a good D/A processor (though Robert Harley tells me that the phase-locked loop that reclocks the datastream in the common Yamaha S/PDIF receiver chip is specified at no better than 5ns jitter). An FFT program was then used to examine the spectra of these signals, which are shown in figs.1 through 5.
Figs.1-4 show the effect on a 10kHz signal at the 16-bit system's maximum level (0dB) of jitter having this 1kHz periodicity. Fig.1 shows the spectrum of the pure 10kHz signal with no jitter. A single spike at 10kHz rises above noise components that lie between 112dB and 122dB down. (Summing all these noise components in an RMS manner will give the theoretical 98dB dynamic range of a 16-bit digital audio system.) The curve in fig.2 has had 2ns p-p of 1kHz jitter applied to the data. While the noise components remain the same in level, note that sidebands at 9kHz and 11kHz have sprung up on either side of the fundamental, at -83.9dB and -84.4dB respectively. This 1kHz spacing is, not coincidentally, the exact frequency of the jitter signal. Manipulating the purely digital data has therefore changed the final analog signal, something that the "bits-is-bits" school of commentators would have you believe to be an impossibility. Figs.3 and 4 show the effect on the analog spectrum when the jitter amplitude is lowered, first to 0.4ns (400ps) and then to 40ps—40 trillionths of a second! With reducing jitter amplitude, the sidebands drop until they eventually disappear back into the 16-bit noise floor.
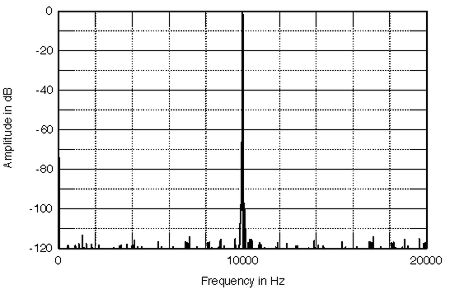
Fig.1 Simulated effect of 1kHz jitter on a 16-bit ADC with a 10kHz tone at 0dBFS sampled at 44.1kHz; zero jitter.
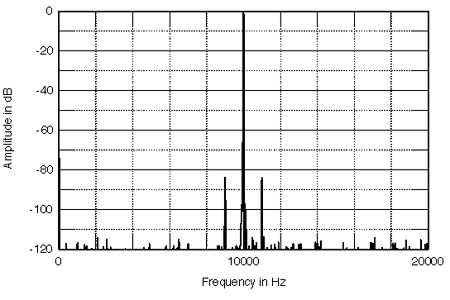
Fig.2 As fig.1 but with 2ns p-p jitter.
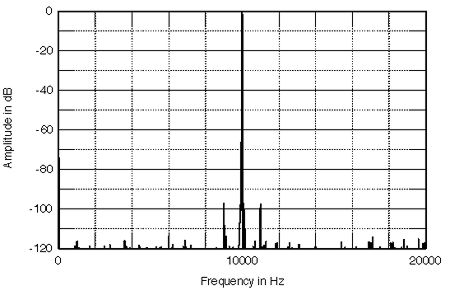
Fig.3 As fig.1 but with 400ps p-p jitter.
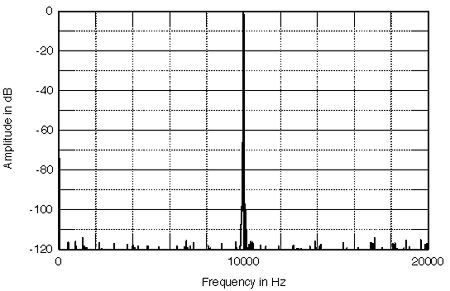
Fig.4 As fig.1 but with 40ps p-p jitter.
Fig.5 shows what happens to the sidebands when the 1kHz jitter amplitude is kept constant and the signal is reduced in level (the sidebands drop with the signal, keeping the same -84dB relationship), while fig.6 shows what happens to a 0dB, 10kHz signal when the jitter signal is changed from a pure tone (which is unlikely) to random (white) noise. By comparing fig.6 with fig.1, it can be seen that the addition of 2ns' worth of jitter has lifted the entire analog noise floor by 10dB. In other words, 2ns of p-p noise jitter reduces the simulated signal resolution from 16 bits to less than 15! (Footnote 3)
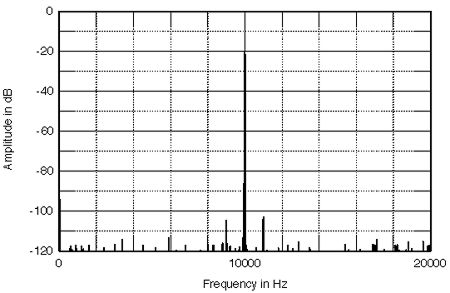
Fig.5 Simulated effect of 2ns p-p, 1kHz jitter on a 16-bit ADC with a 10kHz tone at -20dBFS sampled at 44.1kHz.
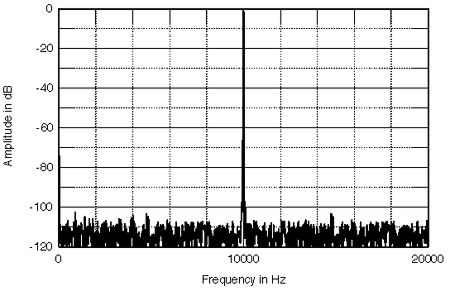
Fig.6 Simulated effect of 2ns p-p, white-noise jitter on a 16-bit ADC with a 10kHz tone at 0dBFS sampled at 44.1kHz.
If you think about it, it is to be expected that digital-domain jitter prior to the DAC will produce effects in the analog domain. With data representing a sinewave signal, every time the sampling instant is late it is as though the shape of the reconstructed sinewave has bulged out a little at that instant. Conversely, if the sampling instant is early, the final sinewave shape will appear to have been sucked in a little. For a given sample time indeterminacy, the relative effect of that bulge or depression in the sinewave shape will be greater the higher in frequency that sinewave. Data jitter therefore has a more severe effect on high than on low frequencies.
A shape change on a sinewave is the fundamental description of analog distortion, and with jitter can be seen to produce an effect very similar to classic frequency modulation. In the case of a pure noise jitter, the reconstructed sinewave shape will be overlaid with that noise, giving the reduction in dynamic range seen in fig.6.
Are these effects audible?
At the 1990 AES Convention in Montreux earlier this year, I sat in on a workshop examining the audibility of peculiarly digital distortion, including the effects of jitter. On pure high-frequency tones, low levels of sinewave jitter could easily be heard. Jitter, however, is unlikely to consist of a pure sinewave applied to the data; it will more likely have a noise-like character. In addition, the data in a CD player are reclocked with crystal precision from a FIFO (first-in, first-out) RAM buffer, or have the clock signal extracted and stabilized with a phase-locked loop (PLL) in a D/A processor. Any jitter produced in the datastream by the CD player's laser pickup or present in the data output by the transport feeding the processor will therefore be very much reduced in level (footnote 4). (Though any jitter introduced at the time of the original A/D conversion will be treated as an intrinsic part of the signal, as in my simulations above, and will be preserved intact.)
Nevertheless, these results tie in with work by others that indicates that 16-bit data jitter of any kind needs to be less than 200ps or so if it is not to produce measurable effects in the analog signal (footnote 5), which in turn means that even though the data are reclocked, the crystal clock in the CD player or the PLL in the processor that do that reclocking need to hold their word-to-word timing accuracy to better than 10 parts in a million. And that time precision needs to be preserved during the digital data's travails on its way to the DAC, something that in my opinion is, frankly, unlikely.
The audible effect of jitter suggested by these simulations would be to add a signal-related grundge and lack of resolution as the analog signal's noise floor rises and falls with both the signal and the jitter, while any periodicity in the jitter—at the power-line frequency and its harmonics, for example—will throw up frequency-modulation sidebands around every spectral component of the music. The "clean" nature of the original analog signal will be degraded, "fuzzed up" if you like, to produce the typical, flat-perspectived, often unmusically grainy CD sound.
Does anyone still feel that "bits is bits"? With jitter applied to the datastream, bits may indeed still be bits, but only if you never convert them to analog—a truly Zen situation!
Footnote 1: In Stereophile Vol.9 No.2, March 1986, where he said in his interview with J. Gordon Holt (p.110) that "One least significant bit of amplitude is equivalent to 200 picoseconds of time...if the timing is off, the output...will not correspond in amplitude to the digital code."—John Atkinson
Footnote 2: "The Effects of Sampling Clock Jitter on Nyquist Sampling Analog-to-Digital Converters, and on Oversampling Delta-Sigma ADCs," Steven Harris, JAES, July/August 1990, Vol.38 No.7/8.—John Atkinson
Footnote 3: In his paper, Dr. Harris examined whether his simulations were correct by building an experimental setup whereby precisely known quantities and types of jitter could be injected into an A/D circuit. The measured effects corresponded very closely to those predicted by the program.—John Atkinson
Footnote 4: It is more accurate to say "filtered" rather than reduced, as each data recovery scheme low-pass filters the jitter rather than eliminates it.—John Atkinson
Footnote 5: Although other writers have felt that bit-bit jitter is important, I can't see that this matters, as all this affects is the exact time the stream of 16 ones and zeros is fed into the DAC's serial-to-parallel input register. A one remains a one and a zero a zero; in this respect, the "bits is bits" proponents are correct. Consider an abacus: it makes no difference to the result how fast, how slow, or how unevenly its user manipulates the individual beads. All that matters is the final state of those beads. If you need your abacus to produce its answer at a specific instant, however, then any variation in that time will have an effect. Similarly, jitter in the word-word timing, which will affect the exact time at which the DAC puts out its analog voltage or an ADC takes its analog sample, and which has been examined in this appendix, seems to me to be what is important here.—John Atkinson
- Log in or register to post comments