| Columns Retired Columns & Blogs |
Katz's Corner Episode 21: How Insensitive! Part 3

This story originally appeared at InnerFidelity.com
How Insensitive! Part 3: The Measurements
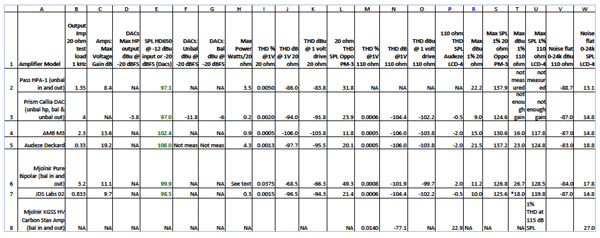
May I have a drumroll, please! Here is the expanded amplifier measurement chart, presenting the essential measurements in a way that consumers can actually use, without forcing them to become engineers. At first it appears to be a daunting looking chart, but consumers will be presented with only a few of these measurements.
Figure 1: Essential Measurements of seven headphone amplifiers. (Click on image to load a .pdf for better viewing.)
The Pass
I added one amplifier to this discussion which I did not measure, the Pass HPA-1 (row 2), and used John Atkinson's measurements from Stereophile with some math to fill in the columns. Its output impedance (column B) is 1.35 Ohms, which implies it uses moderate but not excessive negative feedback. It has good Voltage gain, as seen in columns C and E. It has extremely low THD+N at 1 Volt, 1 kHz, 0.005% (column I), which means the partials plus the noise produce a remarkably low level of -83.8 dBu (column K). That level would produce only 18 dB SPL from an LCD-4, which I did not include in the spreadsheet, because John used a 20 Ohm load and did not verify performance with medium or high impedance loads. I did report (column L) that an Oppo PM-3 would produce 32 dB SPL with this THD+N.
It's fair to ask if 1 Volt is a suitable level for headphone amplifier testing? 1 Volt would drive an Audeze LCD-4 to 104 dB SPL, which seems rather high compared to normal listening levels. But historically, 1 Volt out of a preamplifier into a "typical" power amplifier and "typical" loudspeaker, would also end up with 104 dB SPL*. So 1 Volt is very congruent with the loudspeaker world. Furthermore, if the headphone amplifier has low distortion at 1 Volt, it should perform even better at lower levels, provided it's Class A biased at low levels. So we should also test its distortion at low levels, since with headphones the ear will easily detect low level details more than with distant speakers in a room.
The amplifier's noise floor (columns V and W), -88.7 dBu, would produce an incredibly low 13.1 dB SPL with the LCD-4s, likely inaudible. I reported this, assuming that the amp will present similar noise with a 110 Ohm load. John's measurement was unweighted, wide band, which makes this performance even more remarkable. But my measurement interface, the Prism Lyra, uses a noise-shaped ADC that has a distinctive rise above about 40 kHz, which strongly contributes to a wideband measurement, so I have limited my own noise measurements to between 0-24 kHz in rows 3 through 8.
This amplifier's maximum output at nominal clipping (1% THD) would be able to deliver a deafening 124 dB SPL into the LCD-4, probably a bit more since John measured with a 20 Ohm load. In Column S, we see that at its maximum, the amp can deliver 138 dB SPL to the highly sensitive Oppo PM-3. Take caution when adjusting this amplifier's volume when using a sensitive headphone! I can't wait to audition this amp, which is scheduled to arrive soon for evaluation.
The Callia Headphone Amp
The Callia's (row 3) internal headphone amp's output impedance, which I did not measure, is specified as 4 Ohms (column B). It produces good output level from its internal DAC at maximum headphone gain and volume (columns D and E).
For my distortion measurements, I used THD instead of THD+N. The Lyra ADC's rising noise floor cica 40 kHz would mess up a THD+N measurement as well as a noise measurement. I believe that THD is a more effective measure than THD+N, because we are looking at just distortion products related to the signal, and the noise doesn't interfere. We never have to second guess a distortion measurement made at low levels, which are often dominated by noise. So when I use the term "THD" it means "total harmonic distortion without noise". When I performed a THD+N measurement, all of my amps showed 0.023%, due to the high frequency noise of the Lyra ADC, not actual noise or distortion from the device under test, so I switched to THD. I measured a very low 0.002% THD from the Callia amp at 1 Volt (column I). This translates to an astoundingly low THD floor of -92 dBu (column K).
Unweighted noise within a 24 kHz flat bandwidth (columns V and W) equates to 14.8 dB SPL from the LCD-4s, likely inaudible.
In column S, we see this amplifier's max SPL at clipping with a 20 Ohm load would produce a very loud 125 dB SPL from the sensitive Oppo PM-3. When I increased the load to 110 Ohms, I could not drive the Callia amp into clipping, so the Callia headphone amplifier will not clip into a medium or high impedance. These specs are all very good, and bring up obvious questions as to why I rated this headphone amp so low in the listening tests. I don't have a good answer to that question at this time. We have to look at other objective measurements to get past this mystery, perhaps multitone measurements or some genius out there has an objective answer.
AMB M3
This amp (row 4) has a very good reputation, and is a good kit to build if you have experience soldering and a good technical mind to follow the complex build instructions. But the hidden cost of build time, finding and buying parts probably would be better put into a $2100 amplifier like the Mjolnir Bipolar. I measured a 2.3 Ohm output impedance using a 20 Ohm load with a 1 kHz sine wave, reflecting the moderate amount of negative feedback in this amplifier, the output impedance of the Mosfets and the small buildout resistors. In its +10 dB gain position with the volume control at maximum, it has plenty of Voltage gain (columns C and E) to drive insensitive headphones. I measured a very low 0.0005% THD (that's right, five ten-thousands of a percent) at 1 Volt drive, 1 kHz, regardless of the load. Its max output at 1% THD into 110 Ohms equates to 118 dB SPL from the LCD-4s (column U), which could explain why this amp has such good sonic impact on transient peaks. Or maybe its impact is due to some other factor—like its solid, discrete regulated power supply, or perhaps some distortion that gives it a bit of a perceived sonic edge. We must not discount the fact that subtle distortion can increase the perception of impact, as long as it is not too much. Because distortion is compression.
Audeze Deckard
In contrast with the AMB, this amp (row 5) is all-discrete, class A biased, as testified by the very hot, substantial heatsinks. Its output impedance (column B) is the lowest of the seven amps at 0.33 Ohms, so it must use considerable negative feedback. In columns C and E we can see that the Deckard, in its highest gain position at maximum volume, has more than enough Voltage gain. I measured 0.0013% THD with 1 Volt drive, 20 Ohms (column I), which equates to a low 20 dB SPL from the Oppos (column L). Into 110 Ohms, its THD is even lower, 0.0005% (column M), equivalent to a vanishingly low -2 dB SPL (wideband) from the LCD-4 (column P) summing just the partials without the noise. Its noise (columns V and W) is -83 dBu (0-24 kHz), equating to a very low 19 dB SPL from the LCD-4s. Keep in mind that single-number specs are rough indicators, far more revealing would be a spectral display of the distortion products, which I did not produce for this amplifier.
The Deckard's clipping point into 20 Ohms (column R) is only bettered by the Pass, and by less than a dB. It can produce a whopping maximum of 125 dB SPL from the insensitive LCD-4s (column U). Since this amp has far more sonic impact than the previous units, I'm beginning to see a pattern: high headroom seems to translate to more listening pleasure. But there is a such thing as overkill: I do not understand why Audeze feel an even more powerful amplifier (The "King", 6 watts per channel into 20 Ohms) would be more suitable for the LCD-4s. I'll be happy to audition a King amp in the future!
Mjolnir Pure Bipolar
Spritzer of Mjolnir Audio has informed me that this amplifier was not optimized to feed very low impedances. I don't have a balanced cable for any of my low impedance phones, so I haven't auditioned low impedance phones with this amp yet. Looking at Voltage or dBu measurements into a 20 Ohm load would be misleading: While it cannot deliver the same Voltage into 20 Ohms as the other amps in this list, its performance indicates it would deliver excellent level into a sensitive low impedance phone. Because of this we must concentrate on the SPL that would be delivered into a particular impedance load (Columns S and U).
For example, in column T, we see that this amplifier can produce a whopping 26.7 dBu into 110 Ohms at clipping, exceeding the Pass by about 4 dB! This is the equivalent of a deafening 128 dB SPL from the LCD-4s. Reducing the load to 20 Ohms, its clipping point reduces, but it would still yield 127 dB SPL from the Oppo PM-3 (column S). That's higher than the 20 Ohm maxima of two other amps in that column. Its 1 Volt THD into 20 Ohms is the highest of all the amplifiers, but extremely respectable, 0.0375% (column I). Once the load impedance has risen somewhat higher than 20 Ohms, its distortion drops by two whole orders of magnitude (34 dB)! Column M shows that it has dropped to 0.0008% (this is not a typo) into 110 Ohms. These extreme headroom measurements correlate with the impacting sound quality that I heard in the listening tests. I do not listen loudly—we are speaking about the clarity of unclipped, undistorted short-term transients.
I measured some additional attributes of a few tantalizing amplifiers. The Pure Bipolar's crosstalk, left to right at 20 kHz is very good, 85 dB (not shown). My measurement system is limited to frequencies below about 90 kHz due to its 192 kHz sample rate. The Bipolar's frequency response (Fig. 2A) is effectively ruler flat from 10 Hz to 20 kHz, and less than 0.2 dB down at 60 kHz, so its warm sonic character cannot be "blamed" on frequency response. The noisy looking trace and rise above 60 kHz is probably due to interchannel high frequency noise leakage within the Lyra interface as I use an interchannel transfer function to measure frequency response. Still there is no more than an 0.4 dB rise shown at 80 kHz. To be sure, I performed square wave testing to look for oscillations, and found its square wave responses (not shown) to be textbook-perfect, so I am confident the amplifier is stable.
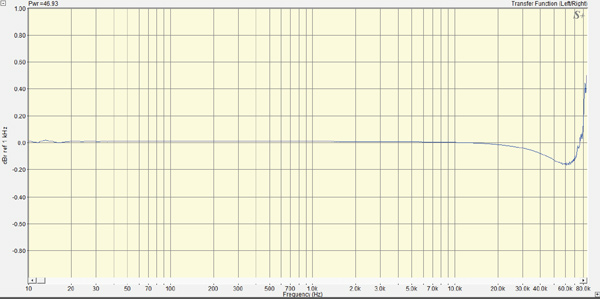
Fig. 2: Mjolnir Pure Bipolar, left channel frequency response
JDS Labs O2
This amplifier (row 7) measures very well. Its output impedance is 0.833 Ohms, the second lowest in the group. Its Voltage gain, seen in columns C and E, is more than adequate. I measured 0.0015% THD at 1 Volt into 20 Ohms, equivalent to 21.4 dB SPL from the Oppo (columns I and L). Its noise floor, without signal, into a 110 Ohm load would yield an even lower 14.8 dB SPL from the LCD-4, probably inaudible (column W). Its maximum output at clipping into 20 Ohms is +10 dBu, which would produce 126 dB SPL from the Oppo (columns R and S).
With a 110 Ohm load, I could not clip the amp sourced from the Callia's unbalanced output since the amp did not have sufficient Voltage gain, but we can say for sure that it clips higher than +18 dBu, which would yield at least 120 dB from the LCD-4. This is respectable headroom and does not explain why in the listening tests I felt this amp constricted transients.
Fig 3 is a graph of the O2 amp's 1 kHz harmonic distortion, at the equivalent of 97 dB SPL, LCD-4 measured into a 110 Ohm load. The only partials are second and third harmonics, which are very low, below negative 14 dB SPL, certainly inaudible. So it has impeccable distortion performance, at least at 1 khz. But consider that its second and/or third harmonic distortion is so low that it may not mask other, undesirable harmonics, perhaps when multiple frequencies are being played (music). My theory is that this performance will make this amp sound dry.
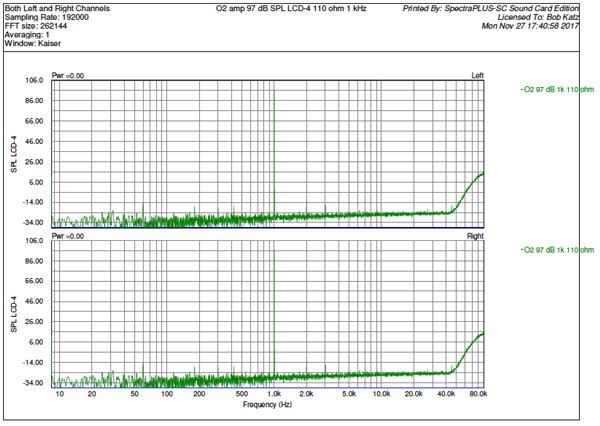
Fig. 3, JDS O2 Amplifier, 1 kHz at the equivalent of 97 dB SPL from an LCD-4 headphone.
Mjolnir KGSS Carbon HV
Measuring a Stax amplifier (row 8) is a bit of a challenge. I had to build a special jig which terminates the amplifier in a balanced 170 kOhm resistive load, the stated impedance of an SR-007. But this is not authentic since the headphones present a capacitive load which is specified by Stax as 170 kOhm at 10 kHz. Perhaps someday I can construct a load that emulates the complex impedance of the Stax. This jig attenuates the high voltage output of the amp to normal voltages and presents a low output resistance to the measurement gear so we can measure it without cable-induced high frequency losses. I wonder if this is the first time that an independent reviewer has published performance measurements of a Stax amplifier.
I did not measure output impedance as I prefer to stay away from high Voltages. Besides, it's an amplifier, and we would expect its output impedance to be a small fraction of 170 kOhm. Voltage is irrelevant to our needs, so I converted all my readings to SPL based on the manufacturer's specifications of 100 Volts RMS yielding 100 dB SPL.
Though higher than any of the other amplifiers, this amplifier's THD measures an excellent 0.0140% at the equivalent of 100 dB SPL (column M). Noise, measured unweighted, 0-24 kHz, is equivalent to a fairly-low 27 dB SPL (column W). I do not hear any hiss or hum from this amp. Output at clipping (1% THD), is equivalent to 115 dB SPL (column U), which is 13 dB lower than the clipping point of the Pure Bipolar with the LCD-4. But I did not sense any loss of headroom or impact in this listening test nor in the detailed shootout I performed in Episode 18. Could this be because the Stax is so "fast" and its diaphragm so light? Or simply that, as common sense would tell us, 115 dB SPL maximum level provides more than enough headroom for any headphone or amp.
Let's look at some graphs of this amplifier's performance, taking advantage of my special new measurement jig. Its frequency response, Fig 4, left channel shown, is identical to the right. As before, the anomalies above 70 kHz are due to high frequency noise in my interface. The response is effectively ruler flat rolling off from 10 kHz to -0.1 dB at 20 k. It gets no lower than about -0.60 dB circa 70 kHz. This amp has very flat and extended response, though to my experience, even 0.1 dB loss at 20 kHz can influence sound quality. In the case of bright Stax headphones, that could be a very good thing.
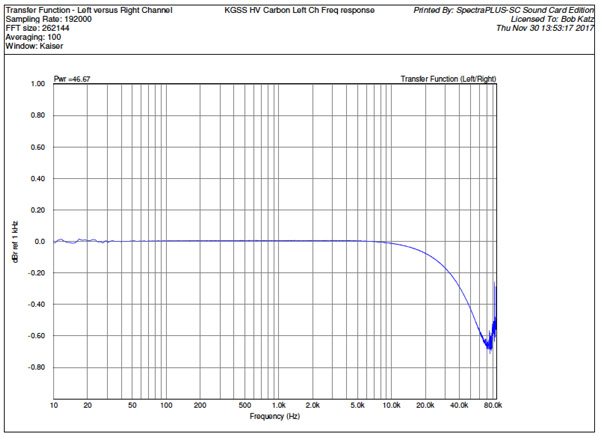
Fig. 4. KGSS HV Carbon Stax amplifier frequency response, left channel
SpectraPlus SC is working on a sweep performance of THD without noise for me, so right now we'll have to live with measuring its THD+N performance from 20-20 kHz (Fig 5). THD+N performance at 100 dB SPL, is extremely linear across the frequency spectrum, measuring around 0.2%, pretty much identical in both channels.
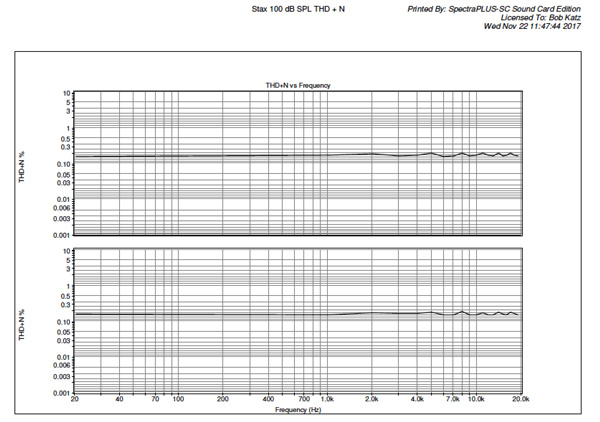
Fig. 5: Mjolnir KGSS HV Carbon THD+N vs. Frequency at 100 dB SPL
This amp's IM Distortion is also impeccable, measured with 19 & 20 kHz at a 1:1 ratio at an approximate equivalent SPL equivalent of 100 dB (Fig. 6). Ignore the red traces, those are peak holds that I forgot to turn off before I took the screenshot. The first order 1 kHz difference product is a very low 25 dB SPL, 75 dB below the fundamentals. There are no other obvious IM artifacts, except for sum products circa 40 kHz. We also see 60 Hz Hum at the extremely low equivalent of 10 dB SPL, quite inaudible, and the third harmonic of the hum, 180 Hz, sitting near the grass at 0 dB SPL. Later, I discovered that the shield of my test cable had come ungrounded, so after grounding the shield, these already-inaudible hum notes dropped right into the grass!
The amplifier's noise components in any frequency are sitting at the equivalent of -10 dB SPL (that's "minus 10 dB SPL") reflecting its completely inaudible noise floor. Dropping the level 10 dB, at an equivalent of 90 dB SPL (not shown), the IM components have almost completely disappeared, so these distortions are likely inconsequential to the sound.
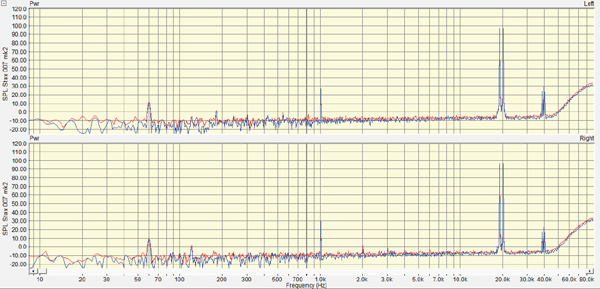
Fig. 6: Mjolnir KGSS HV Carbon 19 & 20 KHz IM distortion at 100 dB equivalent SPL
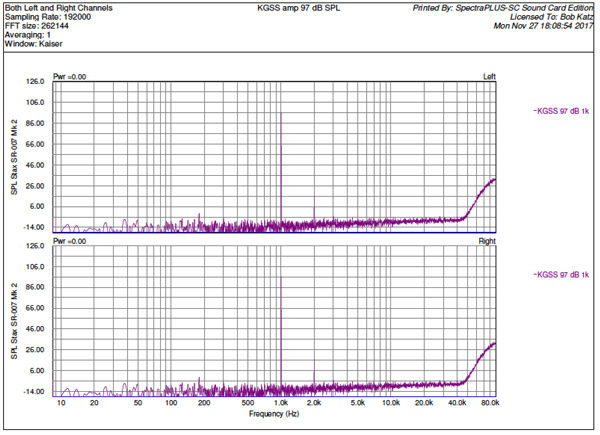
Fig 7: KGSS amp THD+N, 1 kHz at 97 dB equivalent SPL
THD+N at 1 kHz at the equivalent of 97 dB SPL is particularly interesting (Fig. 7), since it consists entirely of second harmonic at an equivalent level of 16 dB SPL, 81 dB below the fundamental. Also notice that with shield connected, hum components move into the grass, with 180 Hz barely peeping through. The rise above 40 kHz is the noise of the Lyra interface's noise shaped ADC.
Is this second harmonic audible? At 16 dB SPL we might not expect it to be, but perhaps this second harmonic subtly contributes to the warmth and sonic beauty of the Mjolnir design, and let's not forget that music consists of many frequencies, so the second harmonics add up, perhaps to something subtly interpreted as "warmth". Ordinarily we should expect to see third harmonic, given the push-pull nature of the device. Perhaps designers Spritzer or Kevin can enlighten us on this measurement. I measured only third harmonic with the Pure Bipolar (not shown).
I'd like to learn about existing research on theories connecting listening experience with measurements. Designers Dave Hill and Nelson Pass assert that controlled amounts of harmonic distortion enhance depth, and are in agreement that too much distortion ruins the picture. In order to prove these contentions, it would be necessary to construct an analog-based distortion generator, that creates controlled amounts of second and third harmonic distortion, and place it in series with an amplifier to see if it improves or deteriorates the sonic picture. This is akin to audiophiles putting tube preamps in front of solid state amplifiers to warm them up.
The KGSS's square wave performance is impeccable (Figures 8, 9, 10), measured with my Fluke Scopemeter and a 10:1 probe. Left channel shown, but right is identical. I want to thank one of my mentors, Jim Johnston, who has just produced for me audio files with theoretically-perfect 24-bit square wave files at 100 Hz, 1 kHz and 10 kHz at 192 kHz sample rate. These digitally-generated, band-limited square waves have all the required harmonic components up to the Nyquist limit, so there would be no aliasing or subharmonics. The overshoot at the head of each transition is a necessary component of a band-limited square wave and comes with the territory. The 10 kHz wave wiggles more because there aren't very many harmonics left above 10 kHz to form a more perfect square shape. All three waves at the amplifier output have symmetrical rise and fall times and slew rates, which is a good sign of a well-designed, perfectly symmetrical amplifier. At 100 Hz, the horizontal line has the slightest tilt, barely noticeable, a sign of an excellent, stable power supply and extended low frequency response.
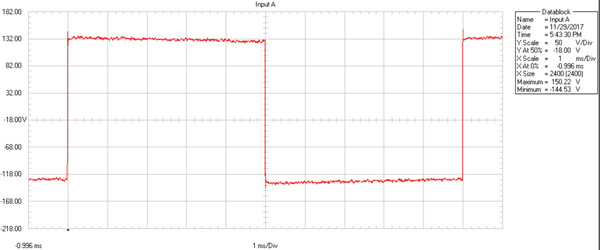
Fig. 8, KGSS HV Carbon, 100 Hz square wave at 250 Volts p-p
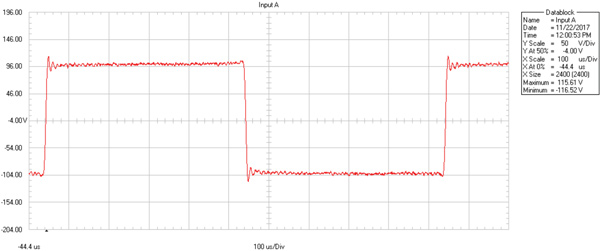
Fig. 9, KGSS HV Carbon, 1 kHz square wave at 200 Volts p-p
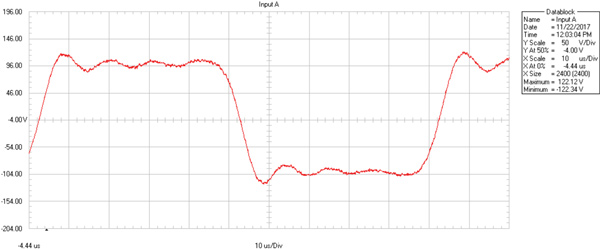
Fig. 10, KGSS HV Carbon, 10 kHz square wave at 200 Volts p-p
What amazes me is that an amp which swings hundreds of Volts can perform as well as amplifiers with only 10 Volt swing. Designers Spritzer and Kevin Gilmore have lots of experience designing high voltage amplifiers, which result in impeccable listening and measurements. This amp measures great and sounds great.
Tentative Conclusion
In the September issue of Stereophile, the venerable designer Nelson Pass speaks of his design philosophy, which relates to some of the issues brought up here. For those curious as to the possible correlation between measurement, design, and sonics, this interview with Pass is a must-read. A year ago I switched my loudspeaker amplification from the rather warm-sounding Lipinski amps to the totally-neutral Atsah 500s, which use Hypex modules. Designer Bruno Putseyz's amplifier philosophy is absolute zero distortion and these Class D amps have no sound of their own. But I believe that my monitoring equipment which is in front of these amps shifts the total sound just that desirable fraction to the warm side while remaining detailed and defined.
I contend that an amp which sounds "dry" must not be accurate. Many "dry" sounding amps also sound a bit harsh. Is this because of extreme negative feedback or an artifact of the negative feedback in relation to the harmonic structure? I'm not the first to claim that when you attenuate the overall distortion into the practically immeasurable, the amplitude of the ugly harmonics can rear their heads by unmasking. Could this be the reason why the O2 and the AMB sound a bit harsh and sometimes bright? Conversely, a little bit of second and/or third harmonic can sweeten the picture without harming the detail. Does that create an amp which is more accurate or simply euphonic? You decide!
* Calculation is based on: Power amplifier with 26 dB Voltage gain. 8 Ohm loudspeaker with sensitivity 87 dB/1W/1 meter. So 1 Volt into the power amplifier would yield 104 dB SPL from the speaker.
- Log in or register to post comments