| Columns Retired Columns & Blogs |
dCS 972 D/D converter Measurements
Sidebar 4: Measurements
It must be clearly understood that upsampling from 44.1kHz to 96kHz or 192kHz doesn't add high-frequency information that was above the Nyquist Frequency—22.05kHz—of the first, lower sample rate.
This is graphically shown in fig.1, which shows the the dCS 972/Elgar's frequency response of the digital signal for three different input conditions. In all three cases, the 972 was set to output a 192kHz datastream to the dCS Elgar, and the Audio Precision System One output an analog sinewave (swept from 20Hz to 100kHz) to a dCS 904 24-bit A/D converter. The widest bandwidth trace, with its -3dB point at approximately 71kHz, is with the 904 set to sample the analog data at 192kHz. The next-widest bandwidth trace is with the A/D converter sampling at 96kHz, with the data upsampled to 192kHz by the 972. This trace's -3dB point of around 40.5kHz is not changed by the increase in sample rate. Finally, the most restricted trace was taken with the 904 sampling at 44.1kHz and the 972 converting that to a 192kHz datastream. Again, the upsampling doesn't add any HF data above the 44.1kHz datastream's -3dB point of 20.5kHz.
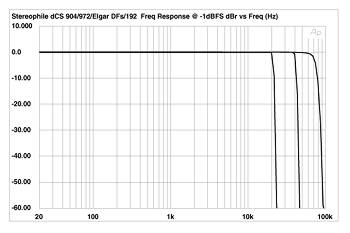
Fig.1 dCS 972, frequency response at -0.1dBFS with data upsampled to 192kHz (from left to right): 44.1kHz, 96kHz, and 192kHz original sampling frequencies (10dB/vertical div.).
So if, as I have heard myself, the upsampled datastream sounds better, it's not because the 972 is adding HF information. If you consider that the digital filters in almost all CD players already resample the 44.1kHz data to drive the DACs at an 8x rate—almost always by interspersing each real data point with seven zero-value samples at the higher rate, a process called "zero stuffing"—I can only assume that the 972 does the upsampling with a greater degree of precision.
One thing I did notice was that there was a slight insertion loss when the 972 was set to upsample the data: -0.04dB when performing a 44.1/96 conversion, -0.16dB with a 44.1/192 conversion. The latter will be just audible.
When the 972 is set to increase the data word length, again, it cannot create new information from a CD Standard 16-bit/44.1kHz datastream. To put the measurements into perspective, fig.2 shows an FFT-derived spectrum of a digital 1kHz tone at -0.1dBFS, sampled at 44.1kHz with a 24-bit word length. (Both digital generator and digital analyzer were implemented with a dual-board PrismSound DScope.) The base of this graph lies at a roots-of-the-universe -180dBFS; the individual components of the noise floor can be seen to lie between -160dBFS and below -180dBFS; their RMS (root-mean-square) sum gives a signal/noise ratio of 144dB, which is way, way greater than can be accommodated by any known recording or playback system. (That doesn't mean that operating digital gear with an internal data path 24 bits wide is not unnecessary.)
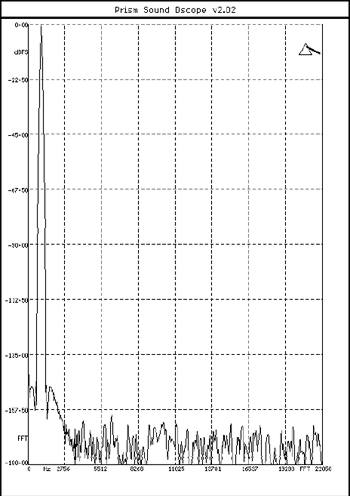
Fig.2 dCS 972, spectrum, DC-22.05kHz, 1kHz at -0.1dBFS, 24-bit word length (linear frequency scale, 22.5dB/vertical div.).
Reducing the bit depth to 20 bits gives the spectrum shown in fig.3. The individual noise components have risen by an average of 24dB, to give an S/N ratio of 120dB, which is close to the limit of current analog design and about the widest dynamic range that can be reproduced in a playback system (not counting stadium-rock PA equipment). Reducing the datastream to the CD's 16 bits gives the spectrum shown in fig.4. Again, the 4-bit reduction of word length results in a 24dB degradation of the S/N ratio, to 96dB.
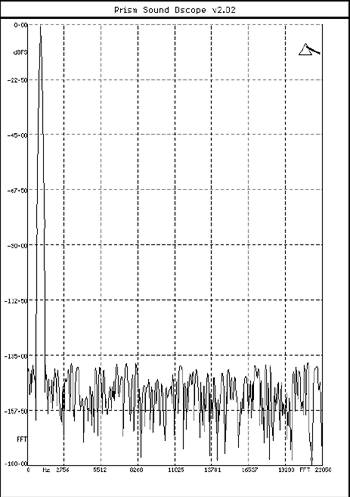
Fig.3 dCS 972, spectrum, DC-22.05kHz, 1kHz at -0.1dBFS, 20-bit word length (linear frequency scale, 22.5dB/vertical div.).
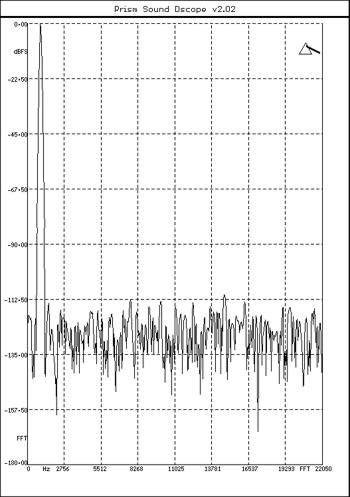
Fig.4 dCS 972, spectrum, DC-22.05kHz, 1kHz at -0.1dBFS, 16-bit word length (linear frequency scale, 22.5dB/vertical div.).
- Log in or register to post comments