| Columns Retired Columns & Blogs |
Carver Amazing Loudspeaker (Platinum Edition) Measurements
Sidebar 2: Measurements
Footnote 1: The truncation of the impulse response data before the first room reflection, that from the floor, means that the FFT-derived spectrum has a resolution of approximately 200Hz.—John Atkinson
As an interested observer during much of Dick's auditioning of the Amazing, and having spent most of a weekend with Bobby the C last September (see my interview with him elsewhere in this issue), I was intrigued to get the final samples of the Amazings into my own listening room for a little measuring fun. Having just installed the DRA Labs MLSSA measuring system in my PC, I felt that this speaker would really give it a workout.
And I wasn't wrong. The Carver Amazing's impedance magnitude and electrical phase, measured with MLSSA, are shown in fig.1. The lower of the two humps is the woofer resonance at 23Hz or so, while the upper is due to the crossover circuit, not to the ribbon suspension resonance. (The impedance of the ribbon alone, not shown, features a smoothly rising impedance below 200Hz.) The sharp peak at 6710Hz is due to the notch filter introduced by Bob Carver in his attempt to reduce the speaker's audible sibilance. All in all, though the impedance doesn't drop below 3.76 ohms, the Amazing's lowish sensitivity means that an amplifier capable of delivering high currents and high voltages will be best suited to drive it.
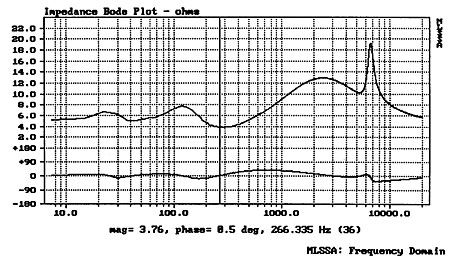
Fig.1 Carver Amazing Loudspeaker, electrical impedance (top, 2 ohms/vertical div.) and phase (bottom, 90°/vertical div.).
Fig.2 shows the anechoic section of the Amazing's impulse response (calculated from the MLS data), measured at a 48" distance, 36" from the floor (a typical listening height), using a calibrated B&K 4006 microphone. (Both controls were set to their 12 o'clock position, which was how DO had preferred listening to the speaker.) The leading edge of the pulse is well-defined, but there then follows a complicated pattern of ringing. The Amazing's ribbon is most definitely not unresonant (though, of course, the resonances may be due to the airspaces in front of and behind the ribbon that are enclosed by the magnet structure). Fig.3 shows the associated step response, which appears to suggest that while the ribbon (the initial right-angle step) is connected in positive acoustic polarity, the woofers are connected in inverted polarity. The smooth hand-over from one to the other, however, suggests good frequency-domain integration between the units.
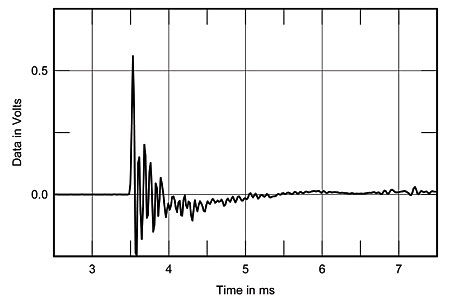
Fig.2 Carver Amazing Loudspeaker, impulse response on ribbon axis. (5ms time window, 30kHz bandwidth.)
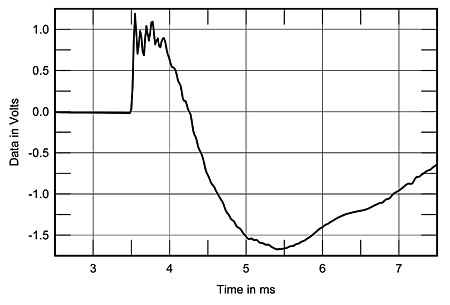
Fig.3 Carver Amazing Loudspeaker, step response on ribbon axis. (5ms time window, 30kHz bandwidth.)
Performing a Fast Fourier Transform on the discrete time-domain data gives the Amazing's anechoic frequency response. I have shown this from 200Hz upward (footnote 1) to the right of fig.4, which was plotted using third-party graphics software rather than that provided by MLSSA, because I prefer Stereophile's published frequency-response plots to have the same aspect ratio and 50dB scaling as the traditional B&K graphs. Obvious features are the downward trend in the lower midrange, presumably due to proximity effect, with then obvious peaks in the 5–6kHz and 11–13kHz regions. No wonder DO found this speaker to emphasize sibilants. (Bob Carver's notch filter appears from this measurement to be both too narrow and too high in center frequency to significantly reduce the energy in the lower of these two regions.)
I also examined the ±15° lateral off-axis behavior of the ribbon; the response was effectively identical on both the woofer and to the baffle-edge sides, suggesting that, though DO found otherwise, the exact toe-in should be relatively uncritical in producing the best tonal balance. Maybe what the toe-in achieves is to affect the audibility of the time-domain problems rather than those in the frequency domain.
The curve to the left of fig.4 is the response of the topmost of the four woofers, measured in the nearfield; ie, with the microphone almost touching the grille cloth. Without the cancellation effect of the finite baffle loading, the intrinsic response can be seen to be centered on the drive-unit's resonance (though this driver's appears to be a little higher than that suggested by the system impedance).
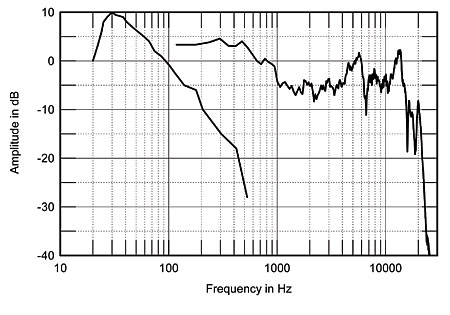
Fig.4 Carver Amazing Loudspeaker, nearfield woofer response (left) and anechoic response on ribbon axis at 48", with tone controls set to 12:00, corrected for microphone response.
It is impossible to estimate from this nearfield measurement what the speaker's true extension would be in-room. I therefore carried out a spatially averaged, 1/3-octave measurement using an Audio Control Industrial SA-3050A spectrum analyzer with its calibrated microphone (footnote 2). The bass can be seen from fig.5 to be elevated by more than 6dB compared with the treble region, with extension really only down to 30Hz. Certainly in my room, the speaker sounded unmusically "slow," which correlates nicely with this measurement. The midrange, however, does feature an exceptionally smooth response trend, suggesting that DO was right on the money when he talked about "exquisite midrange textural smoothness and sumptuous liquidity" in this region.
But oh, look at the treble. There again is the sibilance, as revealed by the MLSSA measurement. Even with totally different measurement hardware, this excess of energy in the 5kHz and 12.5kHz 1/3-octave bands was apparent on every axis; its audible effect was severe.
Finally, one of the beauties of MLSSA is that its post-processing options allow you to look for resonant behavior in a very effective manner. Fig.6 shows the typical "waterfall" display produced as the system analyzes the decay of the impulse sound emitted by the speaker (shown in fig.2) in discrete time slices. Interestingly, the very audible energy excesses around 5–6kHz and 11–13kHz, though presumably due to resonances—note the persistent small ridges in these regions parallel to the time axis—decay reasonably quickly. But note the very long ridges at 1600Hz (the cursor position) and at 1300Hz, which persist in the case of the 1600Hz resonance right out to the 6ms edge of the graph. Though there are only minor peaks in the amplitude response at these frequencies, these long decay times reveal them to be major resonances. Undoubtedly it was their presence that led Dick to feel that "an occasional squawk crept in around 1kHz."
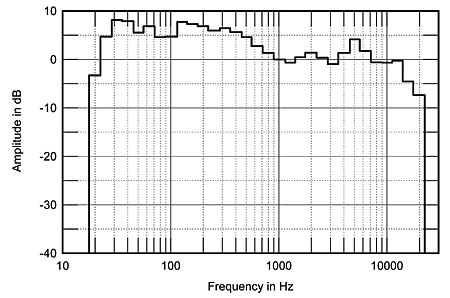
Fig.5 Carver Amazing Loudspeaker, spatially averaged, 1/3-octave response in JA's listening room.
Though these FFT-derived graphs are unreliable below 500Hz or so, due to the truncation of the time-domain data to remove room effects, note that fig.6 does reveal the exaggerated nature of the lower mids, and hints that the bass energy just keeps on a-comin', as suggested by Dick's auditioning, presumably due to the highish-Q LF alignment.—John Atkinson
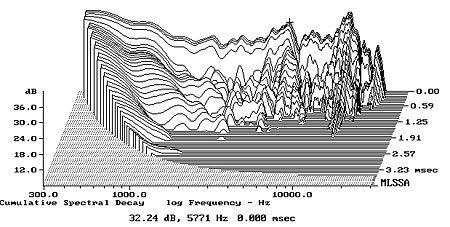
Fig.6 Carver Amazing Loudspeaker, cumulative spectral-decay plot at 48" (0.15ms risetime).
Footnote 1: The truncation of the impulse response data before the first room reflection, that from the floor, means that the FFT-derived spectrum has a resolution of approximately 200Hz.—John Atkinson
Footnote 2: See Vol.12 No.10, October 1989, p.166 for how this test is performed and why I feel it gives a good correlation with the subjectively perceived tonal balance of a loudspeaker.—John Atkinson
- Log in or register to post comments




































