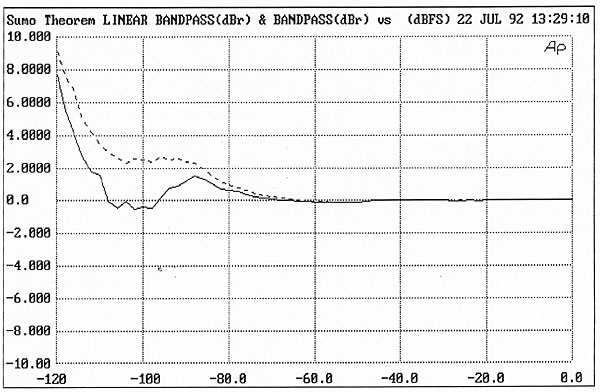
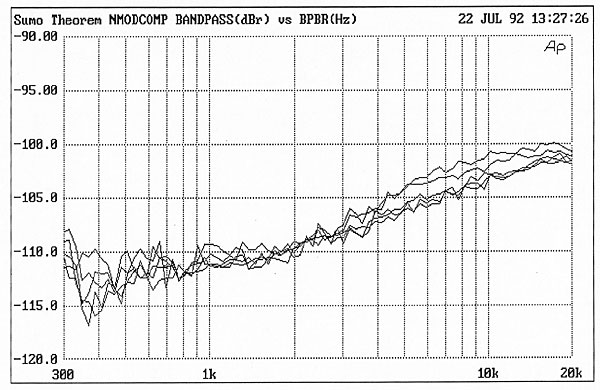
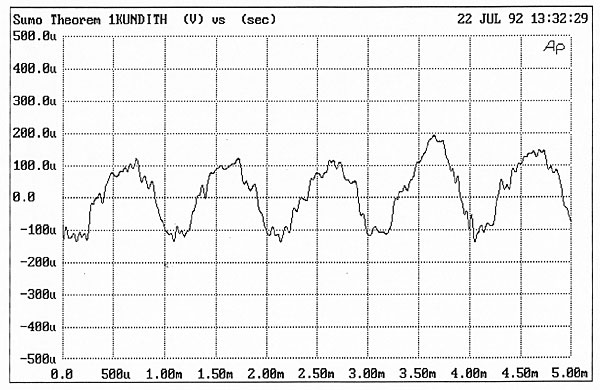
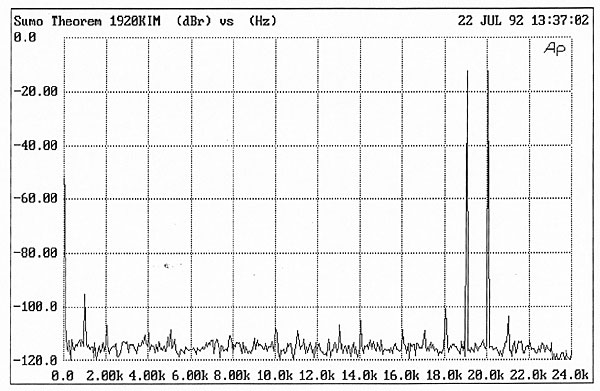
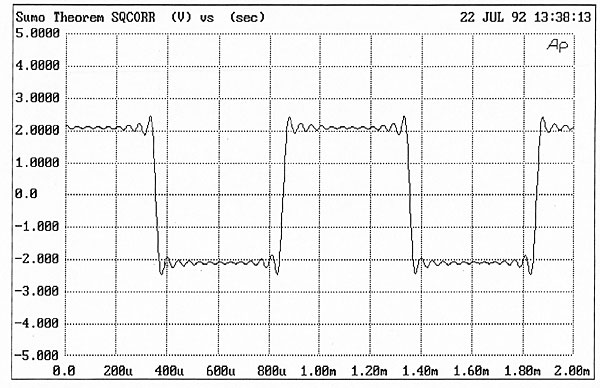
| Columns Retired Columns & Blogs |
... "mediocre" - not even damning with faint praise this time.
$800 would have been much better spent on a Sony CDP-X339ES or, for something different, a Pioneer Elite PD-65, or even a JVC XL-Z1050TN.
https://www.stereophile.com/content/jvc-xl-z1050tn-cd-player