Features

The same type of spectral analysis, but with the processor driven by "digital silence" (all zeros), is also performed and plotted to 200kHz. This test can reveal the presence of spurious junk in or above the audioband, and of such DAC artifacts as self-generated tones (seen as a peak in the trace). Ideally, the trace should be a smooth line, with no peaks at the power-line frequencies and no audioband spikes. The effects of noise-shaping in 1-bit-type converters can also be seen in this measurement as a steep upward slope to the trace. Noise shaping is a resolution-enhancement technique that pushes noise from the audioband into the ultrasonic band, allowing a 1-bit decoder to reproduce the full 16-bit dynamic range of the CD data.

Linearity
Low-level linearity was touted a few years back as the definitive measure of digital-processor performance. While good linearity is a high engineering goal, it doesn't guarantee good sound.

Understanding the concept of linearity is easy: Linearity is how well the processor's analog output level tracks the digital input level. If we put in the code representing a -88dBFS signal, for example, the analog output should be exactly 88dB below its maximum output. Any deviation between digital input level and analog output level is linearity error. Linearity error occurs in all DACs, and is compensated for in many processors by trimming the chip's MSB (Most Significant Bit) at the factory.

Linearity error is expressed as the dB difference between the digital input level and the analog output level at a specific digital level. For example, we may say a particular converter has a "3dB positive error at -90dBFS." This means that when the processor is driven by the digital code representing a -90dBFS signal, the processor's analog output is actually -87dB (3dB higher than the digital input level). Note that the digital input level refers to the signal levels represented by the value of the ones and zeros in the binary code, not the input voltage to the processor's digital input, which remains constant.

A typical linearity plot is shown in fig.6—the dotted trace is the right channel. A perfect processor would produce a ruler-flat line, with no deviation above or below the zero horizontal division. If the trace dips below the center line, this indicates a negative linearity error. If it rises above the center line, the processor has a positive linearity error (the analog output is higher than it should be). The digital input level is read across the bottom, with the highest level at the graph's right-hand side. This particular processor has a negative error of 4.2dB (right channel) and 1.8dB (left channel) at -100dB. [One reason for a DAC appearing to have negative linearity error is that the signal energy is being doubled in frequency—ie, the data represents a 1kHz tone, but the processor puts out a tone an octave higher, at 2kHz. This kind of misbehavior will be seen in the associated -90dBFS spectral analysis plot (fig.7), where the spurious 2kHz component is as high in level as the wanted 1kHz one.—Ed.]

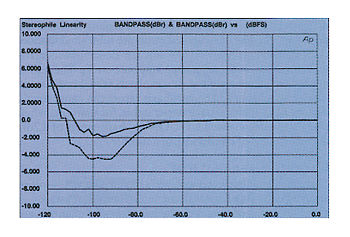
Fig.6 Typical departure from linearity (right channel dashed, 2dB/vertical div.).

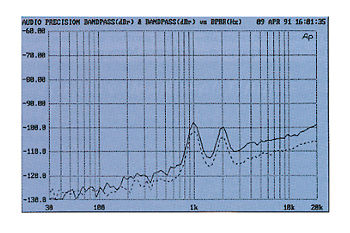
Fig.7 CD player with severe negative low-level linearity error, spectrum of dithered 1kHz tone at -90.31dBFS, with noise and spuriae (1/3-octave analysis, right channel dashed). Note that there's a strong spurious component apparent an octave above the fundamental at 2kHz.

Some processors with excellent low-level linearity appear to have a positive error at very low signal levels (-115dB). This is actually noise swamping the DAC's output. Each measured extension of 6dB below -96dBFS represents an improvement of 1 bit in resolution. The practical lower limit of measuring linearity is about -112dBFS (in quiet processors), representing an effective DAC resolution of just over 18 bits. The 16-bit words on the CD will thus be reproduced with a high degree of accuracy; and if the CD has extra information encoded on it—by Sony Super Bit Mapping or by the Apogee UV-22 and Meridian 618 mastering processors—and if the processor/player's digital receiver and filter chips will pass more than 16-bit words, then that extra signal resolution will result in better CD sound quality.