| Columns Retired Columns & Blogs |
Stereophile's Test CD 2 Tracks 20-26
Track Information, Tracks 20-26, Distortion & Jitter demonstration tracks
Footnote 9: Because of the practical impossibility of us applying specified amounts of jitter in your CD player, this track actually contains the mirror-image situation: the data representing the 11kHz tone have been altered by calculating the effect of the same jitter added at the original A/D conversion. Jitter is jitter, however, no matter where it actually originates, though in this case, the bits are no longer the same bits.
[20] The Harmonic Series, 500Hz fundamental (L+R) (DDD) 0:24
500Hz, 1kHz, 1.5kHz, 2kHz, 2.5kHz, 3kHz, 3.5kHz, 4kHz, 4.5kHz, 5kHz, 5.5kHz, 6kHz, 6.5kHz, 7kHz, 7.5kHz, 8kHz, 8.5kHz, 9kHz, 9.5kHz, 10kHz, at -10dBFS
[21] Second-harmonic distortion (L+R) (DDD) 1:42
500Hz at -10dBFS + 0% second-harmonic distortion (Index 1), then 10%; 0% (Index 2), 3%; 0% (Index 3), 1%; 0% (Index 4), 0.3%; 0% (Index 5), 0.1%
[22] Third-harmonic distortion (L+R) (DDD) 1:42
500Hz at -10dBFS + 0% 3rd harmonic distortion (Index 1), then 10%; 0% (Index 2), 3%; 0% (Index 3), 1%; 0% (Index 4), 0.3%; 0% (Index 5), 0.1%
[23] Seventh-harmonic distortion (L+R) (DDD) 2:02
500Hz at -10dBFS + 0% seventh-harmonic distortion (Index 1), then 10%; 0% (Index 2), 3%; 0% (Index 3), 1%; 0% (Index 4), 0.3%; 0% (Index 5), 0.1%; 0% (Index 6), 0.03%
[24] Typical amplifier distortion signatures (L+R) (DDD) 0:32
500Hz at -10dBFS (Index 1), 500Hz at -10dBFS + tube THD (Index 2), 500Hz at -10dBFS + solid-state THD (Index 3)
[25] Harmonic & sub-harmonic distortion (L+R) (DDD) 0:22
1kHz at -10dBFS pure (Index 1), 1kHz + high-level panel speaker THD (Index 2).
[26] Jitter demonstration track with spoken warning (L+R) (DDD) 0:48
11kHz at -10dBFS (00:12), 11kHz affected by 10ns p-p jitter of 4kHz tone (00:22), 11kHz pure (00:37)
Audiophiles will be familiar with the term "Harmonic Distortion," but how many are really comfortable with what it means? When a signal passes through a hi-fi component, not only will it be reproduced, but so will higher-frequency "images" of that signal at integer multiples of its frequency (track 20). (These are also the notes that a player can produce from a natural horn or trumpet, by varying the tension of his lips.) To show this effect, fig.6 is the spectrum of a pure 500Hz sinewave tone, a single peak being visible at the fundamental frequency. If a hi-fi component adds what is termed "second-harmonic distortion," then it will add a spurious tone at twice the fundamental frequency. This can be seen in fig.7, which indicates 10% of second-harmonic distortion by the peak at 1kHz. Another way of describing this would be to say that the spurious 1kHz tone lies at -20dB (decibels) with respect to the fundamental. This is why the distortion spectra featured in Stereophile and other magazines often have a vertical scale calibrated in dB. Similarly, figs.8 and 9 show 10% of third-harmonic (3 x 500Hz = 1500Hz) and seventh-harmonic distortion (7 x 500Hz = 3500Hz).
Tracks 21, 22, and 23 allow you to compare different levels of second-, third-, and seventh-harmonic distortion with the pure tone, so that you can test yourself as to how much of each kind of distortion you can hear. Make a note at where you can no longer hear any difference between the pure and distorted tones.
In general, the audibility of any particular harmonic will depend on the distance between it and the fundamental on the spectrum's horizontal scale. For manufacturers and reviewers merely to quote a single distortion specification—0.1% or -60dB, for example—is therefore no guide as to whether that distortion will be audible or not (something that Stereophile's founder, J. Gordon Holt, has said for many years). To demonstrate this phenomenon, tracks 24 and 25 compare the sounds of a pure tone with distortion "signatures" typical of a classic tube amplifier near its clipping point (fig.10), an inexpensive class-B solid-state amplifier (fig.11), and a panel speaker near its overload point (figs.12 & 13). (While all these spectra were generated purely in the digital domain by the Audio Precision System One Dual Domain, they were taken from review measurements of real amplifiers and speakers from the last few years.)
The tube amplifier's distortion is high in level, around 3%, and includes some 120Hz power-supply hum, while the THD of the solid-state amplifier is 10 times lower in level, at around 0.3%. Note, however, that the latter is as audible—if not more audible—despite its lower level, because its spectrum favors the higher harmonics. Track 25 is interesting because a panel speaker is a fundamentally chaotic system: when it distorts, it also adds subharmonic and enharmonic components—the mathematician Manfred Schroeder has said that the production of subharmonics was always an indication of chaotic behavior. Normal harmonic-distortion components of the 1kHz fundamental can be seen at 2kHz, 3kHz, 4kHz, and 5kHz, with the third harmonic being the highest in level at -30dB or 3%, but a strong component at half the fundamental frequency can be seen, as well as a couple of enharmonic components between 1kHz and 2kHz. The 500Hz component is 40dB down or 1%, but is very audible because its frequency is lower than that of the fundamental.
A different kind of distortion is that occurring in the digital domain due to timing uncertainty in the datastream. "Bits is bits," say many engineers, but they're really only correct when those bits occur at precisely defined intervals. Any regularly occurring timing imprecision in the digital data words will result in spurious tones appearing in the signal when it is finally converted to analog (see Stereophile, May 1990, pp.49-55 and 81-85; December 1990, p.179; and October 1991, pp.63-69). The effect is worse at high levels and at higher frequencies. To demonstrate this, track 26 offers first a pure tone at 11kHz—Warning: don't play this track too loud—followed by the same tone with the effect of the data words representing the tone being jittered at a frequency of 4kHz (figs.14 & 15, respectively) (footnote 9). Each data word should be precisely spaced at 22µs (0.000022s) intervals; the uncertainly in the data word timing is 10ns (0.00000001s) peak-peak. This is a little higher than that encountered in typical CD players, but it has been exaggerated to make the effect clearly audible. In real life, too, the jitter uncertainty would not necessarily be a pure tone, but a mixture of tones as well as noise and hum. Nevertheless, we hope that you can hear the roughness in the decoded sound of the tone due to a purely digital phenomenon. (If the two halves of track 26 sound identical, then it is likely that the difference is being obscured by high levels of jitter in your player and/or processor.)
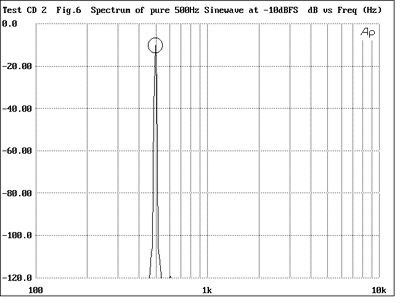
Fig.6 Spectrum of pure 500Hz tone at -10dBFS (100Hz-10kHz)
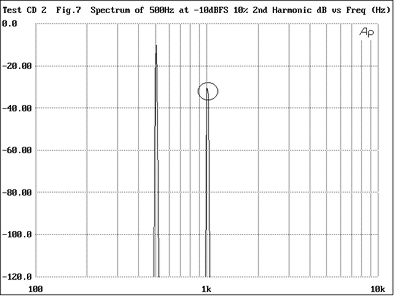
Fig.7 Spectrum of 500Hz tone at -10dBFS with 10% 2nd-harmonic distortion (100Hz-10kHz)
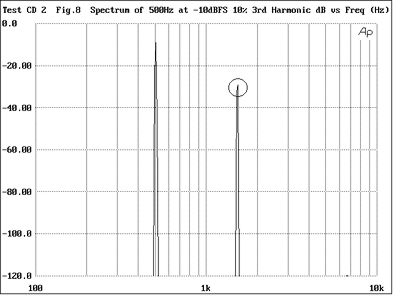
Fig.8 Spectrum of 500Hz tone at -10dBFS with 10% 3rd-harmonic distortion (100Hz-10kHz)
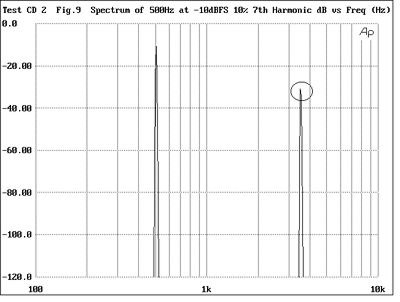
Fig.9 Spectrum of 500Hz tone at -10dBFS with 10% 7th-harmonic distortion (100Hz-10kHz)
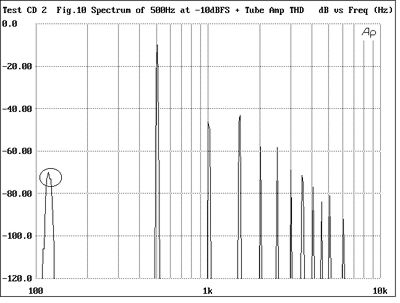
Fig.10 Spectrum of 500Hz tone at -10dBFS with hum and distortion typical of a classic tube amplifier near clipping (100Hz-10kHz)
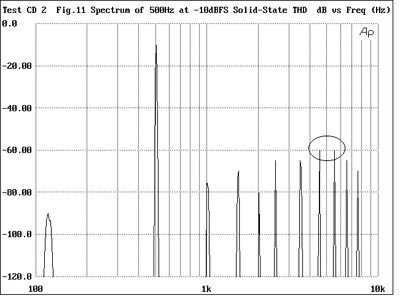
Fig.11 Spectrum of 500Hz tone at -10dBFS with distortion typical of an inexpensive solid-state amplifier operating in class-B (100Hz-10kHz)
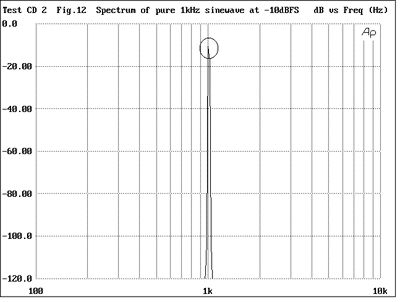
Fig.12 Spectrum of pure 1kHz tone at -10dBFS (100Hz-10kHz)
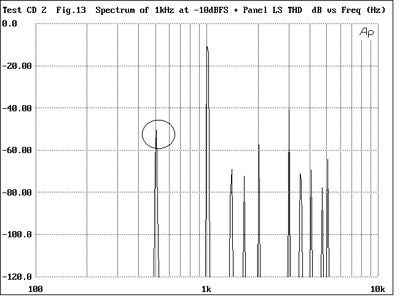
Fig.13 Spectrum of 1kHz tone at -10dBFS with distortion typical of a planar diaphragm near its overload point (100Hz-10kHz)
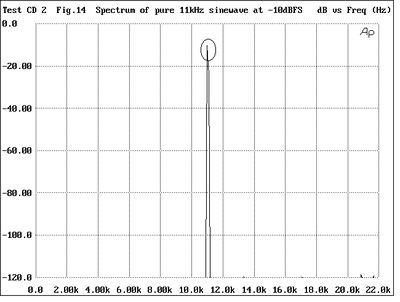
Fig.14 Spectrum of pure 11kHz tone at -10dBFS (1kHz-30kHz, linear frequency scale)
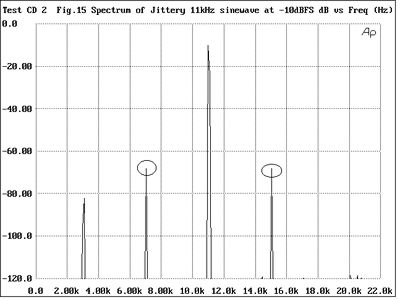
Fig.15 Spectrum of 11kHz tone at -10dBFS, jittered with 10ns p-p of 4kHz (1kHz-30kHz, linear frequency scale)
Footnote 9: Because of the practical impossibility of us applying specified amounts of jitter in your CD player, this track actually contains the mirror-image situation: the data representing the 11kHz tone have been altered by calculating the effect of the same jitter added at the original A/D conversion. Jitter is jitter, however, no matter where it actually originates, though in this case, the bits are no longer the same bits.
- Log in or register to post comments