| Columns Retired Columns & Blogs |
Red Shift: Doppler distortion in loudspeakers Page 2
Prior art
Interest in Doppler distortion began in 1943, with the publication of a paper by two RCA engineers, G.L. Beers and H. Belar, which was the first to identify and quantify this distortion mechanism (footnote 1). Interest in the subjective effects of Doppler distortion intensified in the 1960s with the work of James Moir in the UK (footnote 2) and Paul Klipsch in the US (footnote 3), both of whom concluded that it had a significant effect on speaker sound. But these findings relied in major part on comparisons of speakers with different levels of Doppler distortion, the assumption being that this was their only substantive disparity. As other researchers later argued, this was quite possibly wishful thinking. Other factors may have been responsible for the differences.
Footnote 1: "Frequency-Modulation Distortion in Loudspeakers," reprinted in the Journal of the Audio Engineering Society, Vol.29 No.5, May 1981.
Interest in Doppler distortion began in 1943, with the publication of a paper by two RCA engineers, G.L. Beers and H. Belar, which was the first to identify and quantify this distortion mechanism (footnote 1). Interest in the subjective effects of Doppler distortion intensified in the 1960s with the work of James Moir in the UK (footnote 2) and Paul Klipsch in the US (footnote 3), both of whom concluded that it had a significant effect on speaker sound. But these findings relied in major part on comparisons of speakers with different levels of Doppler distortion, the assumption being that this was their only substantive disparity. As other researchers later argued, this was quite possibly wishful thinking. Other factors may have been responsible for the differences.
The first concerted attempt to sidestep this experimental difficulty was made in the UK by Peter Fryer, who was then working at Rank Hi-Fi (Wharfedale) (footnote 4). In order to be certain that Doppler distortion was the only variable in his listening trials, Fryer built a "Carrier Canceling Doppler Machine"—based on a variable-length, bucket-brigade delay line—to simulate the effect electronically. The conclusion he reached from his listening was that, even when you could hear it, Doppler distortion "is not at all unpleasant up to quite high levels as long as the modulating frequency lies between say 20 and 100Hz," and that "Doppler distortion is unlikely to be of importance in most speaker systems." Detectability, he found, corresponded with a total cone movement (peak–peak) of about 10mm (0.4").
Roy Allison and Ed Villchur later reached broadly similar conclusions using a different experimental technique (footnote 5), although they pointed out that Fryer's detection criterion needed to be relaxed in various ways to reflect real-world loudspeaker use. First, Fryer's work had assumed a full-range drive-unit, whereas most high-quality speakers divide the frequency range between two or more drivers. Second, Fryer had taken no account of the fact that the amount of Doppler distortion generated by a moving diaphragm varies with the angle off the forward axis until, at right angles to the direction of diaphragm motion, it falls to zero. As a result of this, the early reflections and reverberant sound in the listening room contain lower levels of Doppler distortion than the direct sound, which, Allison and Villchur claimed, will further raise the threshold of detection and thus make the generation of audible Doppler distortion by most hi-fi loudspeakers even less likely.
Many loudspeaker designers seem to have taken Allison and Villchur's work as the last word on the Doppler issue. If you search the Audio Engineering Society archives at www.aes.org, you will find that, since that presentation in 1981, no paper on the audibility of Doppler distortion has been presented at an AES convention or published in JAES. But a few audiophiles keep the Doppler flame alight—notably horn aficionados, who, taking their lead from the late Paul Klipsch, claim low levels of Doppler distortion to be one of the reasons that horn-loaded speakers surpass direct-radiating alternatives.
Doppler distortion may have fallen out of the headlines for much of the past 20 years, but, as alluded to earlier, the same cannot be said of another species of frequency intermodulation distortion: jitter. Jitter in digital systems has been a focus of audio-industry attention for well over a decade, and is widely credited with being one of the reasons that digital audio initially had such a bad reception in the audio press. So let's compare the level of FIM distortion introduced by modern digital source components with that generated by analog sources and loudspeakers. Are they in the same ballpark?
Fig.2 does this by combining data from various sources. The blue line shows the proposed tolerance limit for sinusoidal jitter suggested by W.I. Manson of the BBC in the early 1970s, while the red line represents the most stringent National Association of Broadcasters (NAB) standard for wow and flutter in tape machines running at 15ips. Note that, in both cases, the tolerance limit is dependent on the modulating frequency, with much larger amounts of FM distortion being acceptable when the modulating frequency is low—as it will predominantly be with loudspeakers. The black triangles indicate jitter-detection thresholds recorded by eight people, each of whom listened to three different music excerpts in a recent test conducted by Dolby (footnote 6); the solitary pink diamond shows the threshold of detectability of Doppler distortion identified by Peter Fryer.
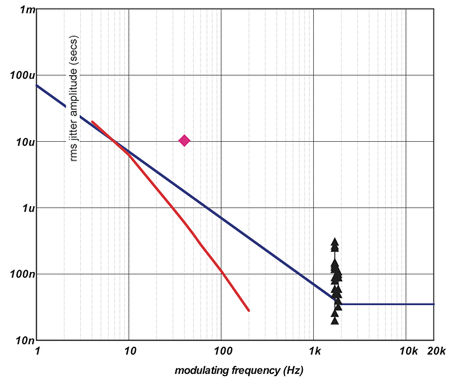
Fig.2 Manson's suggested jitter audibility threshold (blue line), NAB wow and flutter standard (red line), Dolby's jitter listening-test results (black triangles), and Fryer's Doppler audibility threshold (pink diamond).
The fact that all these data agree so well, though they were generated across three decades and in different circumstances, is no more than we might expect, given that the distortion mechanism is fundamentally the same in each case. What will surprise readers who have never seen this information before is how widely these detection thresholds differ from the measured jitter performance of modern CD players, the best of which have total (RMS) jitter levels, measured across a wide frequency range, two orders of magnitude less than anything plotted here.
There are two ways to regard this large disparity. You could conclude that it shows that much of the fuss about jitter is misplaced, and that most modern CD players, even inexpensive ones, generate levels of jitter that are inaudible. But few audiophiles who have heard the sonic improvement that can be wrought by upgrading the clock circuit in many CD players are likely to accept that view. What seems more likely, in the light of their experience, is that fig.2, for whatever reason, doesn't tell the whole story about the audibility of FIM.
As for Doppler distortion, the situation is too complex to be assessed in any meaningful way from this diagram because, in this case, the audio waveform is both the modulating and the modulated signal, which makes this form of FIM unusually complex. The only reliable way to assess whether typical hi-fi speakers produce audible or inaudible amounts of FIM is to listen to music signals with and without representative levels of Doppler distortion added, and to hear if there is an audible difference.
A new experiment
Peter Fryer's hardware approach to Doppler-distortion simulation has the advantage that while listening, you can literally turn a knob to increase or decrease the level of distortion at will. The disadvantage, as with any hardware solution, is that the Doppler engine must be designed, built, and paid for, and you have to make certain it isn't doing anything else to modify the signal other than generating FIM distortion. A software approach that generates preprocessed files for listening, though much less flexible, costs nothing more than the time required to write the code. It is also pretty straightforward to ensure that it behaves exactly as it should.
To simulate Doppler distortion digitally, you must generate output samples where there are no corresponding input samples; in other words, it's a process of interpolation. There are various ways to do this, the simplest of which is first to upsample the input signal by a large factor to generate a much denser grid of sampling points, and then to use linear interpolation to calculate the output value at the precise point it is required. Linear interpolation is inherently inaccurate, but errors can be reduced to an arbitrary level by making the upsampling ratio sufficiently high.
Fig.3 illustrates the worst-case situation for linear interpolation, where the curvature of the signal waveform is at its greatest. For a sinewave, this occurs at the waveform's positive or negative peak, as illustrated. The black curve is the waveform, the red dots indicate adjacent sampling points symmetrically disposed about the waveform's peak value, and the blue dots indicate the interpolated values. Clearly, the error at the waveform peak is the largest. By specifying (1) the amplitude and frequency of the sinewave, and (2) how small we wish the error to be, it is possible to calculate the maximum sample spacing, and hence the sampling rate required to achieve this performance. If we take a full-scale sinewave at 5kHz as our criterion and require the maximum error to be 0.1 of a least significant bit (ie, a tenth of the quantization step size) for 16-bit coding, then the required sampling rate turns out to be 6.358MHz. For test material ripped from CD (as I've used in my simulations), the required upsampling ratio is therefore 144x. To simplify the computation, this was applied in four stages, of 2x, 3x, 4x, and 6x upsampling, respectively.
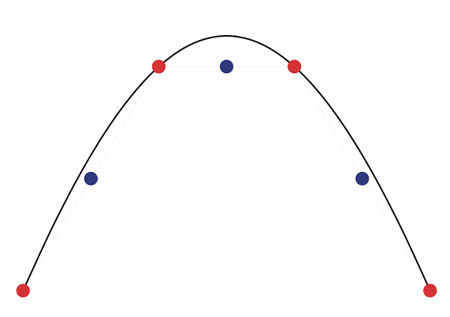
Fig.3 Linear interpolation: the error is largest at the peak of the waveform, where its curvature is highest. Red dots indicate input samples, blue dots interpolated samples.
Each of these upsamplings requires the application of a low-pass digital filter, and these filters should obviously have minimal influence on signal quality. To this end, I designed custom filters with a flat passband to 20kHz and a cube-law rolloff thereafter. (This obviates the passband ripple and excessive time smear of filters designed using equiripple techniques.)
Footnote 1: "Frequency-Modulation Distortion in Loudspeakers," reprinted in the Journal of the Audio Engineering Society, Vol.29 No.5, May 1981.
Footnote 2: "Doppler Distortion in Loudspeakers," Hi-Fi News, January 1967. See also Moir's paper of the same title, presented at the AES 46th Convention, September 1973.
Footnote 3: "Modulation Distortion in Loudspeakers," Journal of the Audio Engineering Society, Vol.17 No.4, April 1969.
Footnote 4: "Simulation and Investigation of Doppler Distortion," AES 56th Convention, March 1977.
Footnote 5: "The Audibility of Doppler Distortion in Loudspeakers," AES 70th Convention, October 1981.
Footnote 6: Eric Benjamin and Benjamin Gannon, "Theoretical and Audible Effects of Jitter on Digital Audio Quality," AES 105th Convention, September 1998.
- Log in or register to post comments