| Columns Retired Columns & Blogs |
Bad Vibes! Sidebar 1
The Rigid Body Concept
The performance of a table-top or platform is a function of the rigidity of the structure and the effectiveness of any applied damping. Each solid object will have many resonant frequencies and associated bending modes. The lower the dominant resonant frequency, the higher the modal displacement. Generally, the first several frequencies/modes are the most significant, and largely define the vibration performance of a given platform. By using materials for constructing audio platforms that are very stiff, the dominant resonances can be shifted to a higher frequency where they are associated with less-damaging, lower-displacement modal activity. In addition, appropriate amounts of damping applied to the platform can further reduce the amplitude of any remaining vibrations over a broad frequency range.
The performance of a table-top or platform is a function of the rigidity of the structure and the effectiveness of any applied damping. Each solid object will have many resonant frequencies and associated bending modes. The lower the dominant resonant frequency, the higher the modal displacement. Generally, the first several frequencies/modes are the most significant, and largely define the vibration performance of a given platform. By using materials for constructing audio platforms that are very stiff, the dominant resonances can be shifted to a higher frequency where they are associated with less-damaging, lower-displacement modal activity. In addition, appropriate amounts of damping applied to the platform can further reduce the amplitude of any remaining vibrations over a broad frequency range.
The performance of a given platform is plotted on a "compliance," or displacement, curve that shows any deviation from an "ideal rigid body"---as defined in the main article. "Compliance" is used rather than "displacement" to show the ratio of displacement to a constant applied force. This curve is represented by a perfectly straight line sloping down the Y axis (representing displacement) from the upper left corner toward the lower right side of a log-log plot, at a slope of -2 across the X axis (representing frequency). This plot shows a platform's actual dynamic response to random vibrations compared to that of an ideal rigid body line.
Fig.1 illustrates the ideal rigid line on the compliance curve. Fig.2 shows a typical dynamic response curve for an undamped table-top and plots the maximum amplification of the first four resonant peaks, labeled A through D, in terms of compliance and frequency. Fig.3 illustrates the relationship between the undamped platform's vibration modes or bending shapes, the corresponding resonant peaks, and the specific frequencies plotted on the curve in fig.2. The scale of the mode shapes in the drawing is exaggerated to better illustrate the bending forces of vibration. Note that dominant peak A is both the lowest in frequency and has the highest displacement or amplitude.
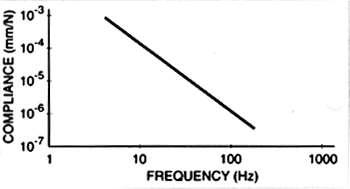
Fig.1 Displacement vs frequency of an ideal rigid body (vertical scale: compliance in mm/N.). Graphic courtesy Newport Corporation.
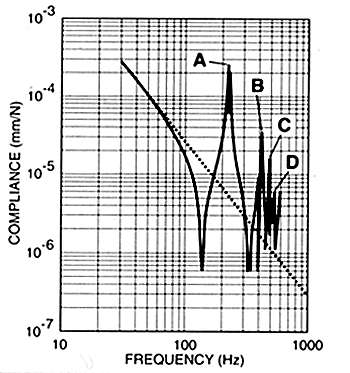
Fig.2 Typical dynamic response of undamped platform to random vibrations. Note deviation from ideal rigid body curve. Letters A-D correspond to vibrational mode shapes shown in fig.3. Graphic courtesy Newport Corporation.
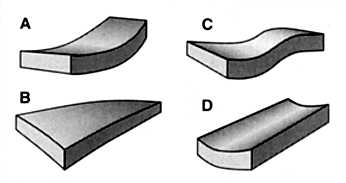
Fig.3 Vibrational modes of platform corresponding to the resonant peaks shown in fig.2. Graphic courtesy Newport Corporation.
Also, displacement decreases inversely proportional to the square of the applied frequency. In practice, a real-world platform will follow the ideal rigid body line up to about 80Hz or so, above which structural vibrational modes are excited and begin to deform the platform's shape. By drawing an imaginary plane through the four platform diagrams, points of minimum motion, called nodes, will be found. Ideally, any coupling devices between a platform and a component or floor should be located at these "quieter points," or nodes.---Shannon Dickson
- Log in or register to post comments