| Columns Retired Columns & Blogs |
Under Pressure: Loudspeakers at Altitude
"The large peak at 16kHz reported by Stereophile...was nowhere in evidence...The most probable explanation of this discrepancy is that the [Waveform supertweeter's] very light ribbon depends on the air load for damping, and that load is much smaller in the thin air up there at 7000' in Santa Fe than at altitudes where less lightheaded and scientifically more accountable reviewers dwell." Thus spake Peter Aczel (footnote 1), erstwhile loudspeaker designer and Editor/Publisher of the reincarnated The Audio Critic, a publication that advertises itself as having "unusual credibility among the top professionals in audio."
Footnote 1: The Audio Critic, Issue 14, Summer through Winter 1989–90.
Normally, when I read such criticism of this magazine's reviews, often based, as is this, on the fact that the writer has published an opinion contrary to ours and therefore feels the need to defend his reputation by attacking ours, I see no need to respond in print. However, as Mr. Aczel does raise a point that I, too, was concerned about when I moved to the high desert from the UK in 1986, I feel the matter worth looking at in more detail, at least regarding high-frequency behavior.
The atmosphere here in New Mexico at 7000'—ca 2150m for all you fellow metriphiles—has a density of 0.9925kg/m3, interpolating between the data given for altitudes of 2000m and 2500m in Shaeffer's and Day's A Field Guide to the Atmosphere (Houghton Mifflin, 1981). This is 18% lower than the air density at sea level and leads to a greater sense of weariness at the end of the working day. Notwithstanding that, I calculated the speed of sound at this altitude to be effectively identical to that at sea level (footnote 2) at 1121ft/s (345m/s) at 72°F (24°C). (Any effect of lower air density on the speed of sound appears to be swamped by its dependence on ambient temperature.) Any acoustic phenomena directly related to the speed of sound—diffraction, interference, etc.—will therefore be the same in Santa Fe as at sea level.
So, how does lower air density affect a loudspeaker's high-frequency behavior?
Primarily, it lowers the efficiency of any pistonic diaphragm. According to the third edition of Martin Colloms's High Performance Loudspeakers (Pentech Press, 1985), the reference efficiency of a pistonic diaphragm (p.27) is directly proportional to the air density and inversely proportional to the square of the moving mass, which includes that of the drive-unit (diaphragm and coil) and the reactive mass of the air load on its diaphragm. The effect of the air density will therefore depend on the drive-unit's design: if it has a high-mass diaphragm, any changes in the air load due to the lower density will be negligible, and the change in efficiency will be directly related to the change in air density.
With moving-coil woofers, where the passband wavelengths are larger than the diaphragm radius, the air load mass is small compared with that of the diaphragm and coil (Martin Colloms quotes 2 grams vs 20gm for a typical 8" plastic-cone driver), and can be neglected. Lowering the air density by 18% will therefore lower the efficiency by pretty much the same 18%. This represents a drop of just under 0.9dB in power terms, meaning that a loudspeaker in Santa Fe needs to be driven slightly harder to reach the same level as at sea level. (Alternatively, you could say that 123W in New Mexico buys you the same loudness as 100W in Florida.)
How about moving-coil dome tweeters? Here the moving mass, typically around 350 milligrams, is considerably smaller than that of a woofer. However, a tweeter's piston radius is also much smaller, generally still being smaller than the wavelength of the emitted sound in the tweeter's passband. (A tone with a frequency of 20kHz will have a wavelength of 17mm or 2/3".) The air load mass will therefore also be smaller, meaning that a conventional tweeter's efficiency will effectively drop by the same 18% as the woofer's. For a conventional dynamic loudspeaker system, therefore, the overall balance between the drive-units will be preserved at the higher altitude.
This has been my experience. When I moved to the US, I brought with me two pairs of speakers featuring typical highish-mass moving-coil drive-units, the sounds of which I was very familiar with: Celestion SL600s and Rogers LS3/5as. Both speakers reassuringly sounded (and measured) the same way in New Mexico as they had back in England.
Where things get trickier is when the driver's diaphragm and coil are low in mass but its radiating area is significantly larger than that of a conventional unit—ribbons of all kinds, electrostatics, and Magneplanar drivers. With these drive-units, it is no longer safe to assume that changes in the air mass loading their diaphragms will be negligible compared with their moving masses. Computing the mass of the air load on a large diaphragm, however, is not as easy as with a conventional drive-unit, due to the fact that one of its dimensions will be larger than the wavelengths of the sound it is emitting. As I understand it, the reactance of the air load will therefore tend to change its value with frequency.
As mentioned by Graham Bank in his interview this month with Robert Harley, there is very little to be found in the literature on the theoretical behavior of such units. In fact, the only papers I could find while preparing this article were by three Sony engineers, on the design of a "leaf" tweeter broadly similar to the Infinity EMIT (footnote 3) and by a Dutch engineer on the design of the recent Philips ribbon midrange- and HF-units (footnote 4). (This Philips tweeter, coincidentally, is the unit used as a supertweeter in the Waveform design, on which Mr. Aczel was commenting.)
The Sony paper, usefully, does include a complete analysis of their ribbon tweeter's behavior, including a table showing how the air load on its diaphragm changes with frequency. It ranges from 14mg at 2.5kHz to 0.6mg at 20kHz at sea level, which would equate to 11.5mg and 0.5mg, respectively, at an altitude of 2150m. (The air load is directly proportional to air density.) The total mass of the diaphragm for this drive-unit (mass of polyimide film plus mass of photo-etched aluminum voice-coil) was stated as being 28mg.
Plugging these figures into the Colloms equation for efficiency mentioned earlier, and hoping that my rusty mathematical skills could be persuaded into action, indicates that at 20kHz, the drive-unit's efficiency will still drop by 17.5% at an altitude of 2150m: ie, it will drop by 0.83dB compared with a moving-coil unit's 0.9dB. However, at the lower frequency, 2.5kHz, the decrease in air mass and reduced damping do compensate to a significant extent for the reduction in efficiency due to the reduced air density. Rather than dropping by 18%, or 0.9dB, it now drops by just 7.3%, or 0.33dB.
When the Sony tweeter is moved to 2150m, it will effectively gain about half a dB in its efficiency at transferring power to the surrounding air at 2.5kHz when compared either with a comparable dome unit at that altitude or its own efficiency at 20kHz. It will presumably, therefore, acquire a slight HF droop at Santa Fe's altitude, though at a maximum of –0.5dB at 20kHz, this is trivial. Note, however, that this is in the contrary direction to Pete Aczel's pronouncement that the ribbon's high-frequency sensitivity increases at higher altitudes.
Experiments
As I postulated above that the primary effect of a decreased air density at Santa Fe's altitude would be a reduction in efficiency of 0.9dB for a conventional moving-coil drive-unit, it seemed obvious to measure the voltage sensitivity of a loudspeaker system in Santa Fe, then measure its sensitivity at sea level. As Tom Norton (who lives in Los Angeles) and I both had access to a speaker that is manufactured to a very tight tolerance, the B&W 801 Matrix, it was feasible to measure each of our samples and compare the results. The two speakers were fed with a 1/3-octave–wide warble tone centered on 1kHz, with the measuring mike at a distance of 1m on the midrange axis. (The influence of the room acoustics with this distance and frequency range is negligible.)
Unfortunately, Tom and I do not have the same spl meters, so the results are only anecdotally comparable. However, with a 1V RMS input to the loudspeaker, Tom's sample at sea level gave an output of either 80dB or 81.8dB, depending on which of two spl meters he used, whereas my sample of the 801 gave 80dB for the same 1V RMS input. The calculated figure of a 0.9dB reduction in efficiency due to a 2150m altitude is therefore probably of the right order.
How about the effect of reduced air density on a moving-coil drive-unit's frequency response? When Tom Norton last visited Santa Fe, he coincidentally brought with him a selection of raw drive-units which we duly measured with the MLSSA system. As I was visiting California at the end of March anyway to attend a social function being hosted by The Absolute Sound and Counterpoint to raise money for the Academy for the Advancement of High End Audio (or AAHEA), I took all the measuring paraphernalia with me so that Tom and I could repeat the measurements under identical conditions apart from the increased air (and smog) density in Los Angeles (footnote 5).
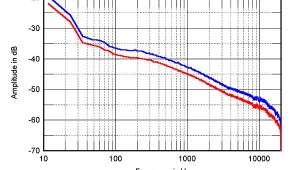
The red trace in fig.1 shows the response of a Focal T120F tweeter, which uses an inverted fiberglass dome, measured in Santa Fe, while the blue trace shows the same tweeter measured in Los Angeles. There appears to be minimal appreciable differences below 20kHz; certainly, it is less than the difference between nominally identical tweeters. You might just notice that the resonant behavior above 20kHz, where the piston radius has become larger than the wavelength, is slightly less well-controlled, presumably due to the lower resistive damping at these frequencies offered by the decreased air load.
Fig.1 Focal T120F measured on-axis at 16" in Santa Fe (red) and in Los Angeles (blue), (no baffle) fed via a series 8µF Wondercap and corrected for microphone response.
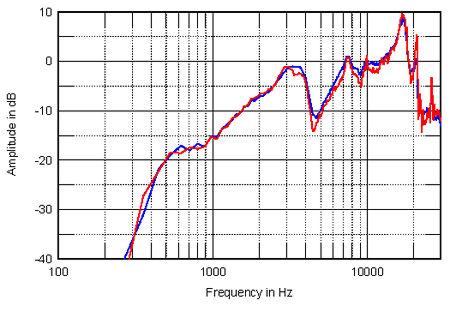
The idea that the reduced air load has less of a resistive damping effect once the piston radius is larger than the wavelength is reinforced by fig.2, which shows the response of an unbaffled 6" SEAS woofer, again measured in Santa Fe (red) and in Los Angeles (blue). The cone's breakup modes above 2kHz can be seen to be slightly accentuated at the higher altitude, though in a real system these would be suppressed by the crossover's roll-off.
Fig.2 SEAS 6" woofer measured on-axis at 16" in Santa Fe (red) and in Los Angeles (blue) (no baffle) and corrected for microphone response.
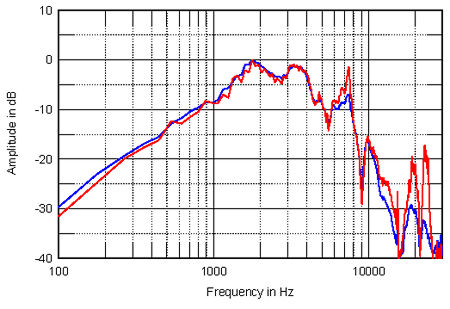
Finally, Snell's Kevin Voecks kindly offered at the AAHEA event to measure a sample of the same Philips ribbon tweeter as used by Waveform at sea level. He would then send me both his measurements and the unit, so that I could investigate how its performance was changed by the altitude. Fig.3 shows the response of the Philips unit in Santa Fe (red) and in Los Angeles (blue), measured on-axis at 20", again without a baffle, with MLSSA set to a 30kHz bandwidth. The measuring mikes were different, of course, though both B&K, and this might contribute to the difference that can be seen above 10kHz, where at the higher altitude, a slight (0.4dB) peak appears, centered on 15.2kHz, with then a faster rate of roll-off, the unit at 2150m being an additional 1.7dB down at 20kHz; rather more than calculated earlier for the Sony ribbon tweeter.
Fig.3 Philips "leaf" supertweeeter measured on-axis at 20" in Santa Fe (red) and in Los Angeles (blue), (no baffle) fed via a series 8µF Wondercap and corrected for microphone response.
Regarding any change in sensitivity, feeding the unit with 1.6V of pink noise at sea level gave an spl of 90.5dB; doing the same thing at 2150m altitude gave an spl of 91dB ±0.5dB, showing that if there is a change in this unit's output, it is probably 1dB or less.
Conclusion
As might seem intuitively obvious, all speakers get quieter with altitude, conventional moving-coil woofers and tweeters pretty much in direct proportion and planars by an amount which will vary with frequency and with the exact ratio between their own diaphragm mass and the air load. It might therefore be possible for a system like the Waveform, which mixes ribbon and conventional units, to change its balance at the higher altitude due to the different drive-units featuring different reductions in their efficiency. That any effect is small, however, was confirmed by measuring both conventional cone/dome units, as well as the Philips ribbon used in the Waveform speaker, at sea level and in Santa Fe.
Even in the worst case, therefore—for example, a design with a conventional moving-coil woofer crossing over around 2kHz to something like the Sony ribbon tweeter mentioned earlier—the resultant mismatch between the two drivers at the crossover point at Santa Fe's altitude will be that the ribbon will play just under 0.6dB higher in level at the bottom end of its passband than the woofer. It would seem that Mr. Aczel's hypothesis, that a planar-type drive-unit will play significantly louder than conventional moving-coil units when the air density is reduced, thus unbalancing a system that mixes both kinds of drive-units, is incorrect.
Regarding the validity of Stereophile's speaker reviews, normal drive-units may be a little less well-controlled above their passbands at our altitude, but the overall tonal balance of a loudspeaker using such units will remain the same. I am forced back to our original conclusion regarding the Waveform loudspeaker: that our sample featured a real 6dB or so boost in the top audio octave that I, at least, felt to render the sound too fizzy. Remember, too, that the speaker's designer heard the speaker in Santa Fe and reassured us that, yes, that was how he intended it to sound.
Footnote 1: The Audio Critic, Issue 14, Summer through Winter 1989–90.
Footnote 2: I checked this figure by looking at the impulse response of the Celestion 3000 loudspeaker reviewed in this issue, which gives an accurate measure of the time it takes for the sound emitted by the loudspeaker to reach the mike, and measuring the physical distance between the ribbon and the mike. The resultant estimate of the speed of sound will be inaccurate only to the extent the acoustic position of the ribbon differs from its physical position and gives a result in close agreement with that calculated.
Footnote 3: "Tweeter Using New Structure and New Material for Diaphragm," Heitaro Nakajima, Masana Ugaji, and Hideo Suyama, reprinted in the Audio Engineering Society anthology Loudspeakers Volume 2, pp.257–262.
Footnote 4: "Compact Ribbon Tweeter/Midrange Loudspeaker," J.A.M. Nieuwendijk, Journal of the Audio Engineering Society, Vol.36 No.10, October 1988.
Footnote 5: Each unit was measured with a 30kHz bandwidth at a distance of 16" on its central axis in free space without a baffle. There will therefore be various suckouts in the response due to reflection of the sound from the edges of each unit's mounting plate. In addition, the tweeters were fed via a series 8µF Wondercap to block low frequencies and DC; this and the lack of a baffle will slope the response down below the treble range, so don't take these measurements as being the true response of the drivers when mounted in a conventional system. All the plots are normalized at 1kHz.
- Log in or register to post comments