| Columns Retired Columns & Blogs |
Bits is Bits? Page 6
In the following tests we introduce sinusoidal jitter to the interface timing by connecting a signal generator to the PLL control voltage. (Note that the PLL control voltage governs instantaneous clock frequency, so we must follow the law of Equation 14 in order to accurately predict injected jitter amplitude.) The DAC output is then digitized using a 16-bit ADC with an independent clock, and analyzed for jitter-related artifacts using a PC.
Footnote 16: Martin Colloms, Hi-Fi News & Record Review, October 1989, pp.83-85.
Fig.26a shows the output spectrum from the test DAC using a 0dBFS, 10kHz CD test tone with no jitter introduced into the interface. (The test unit in this example was the Musical Fidelity Digilog DAC of 16-bit, 4x-oversampling design.) The spectrum is quite pure, with a second harmonic at -96dB relative to the fundamental (the line at 2kHz is due to an idle tone in the ADC). Now consider the measured spectra shown in fig.26b, where 1kHz, 10ns peak jitter has been introduced into the digital datastream, causing sidebands to appear at approximately -73dBFS either side of the fundamental. A second measurement is presented in fig.26c, using the same jitter signal, but this time employing a CD test tone of 2kHz. Both measurements show good agreement with the simulations in terms of both relative levels (within 3dB) and spectral shape, and verify the accuracy of the 100% DAC jitter model.
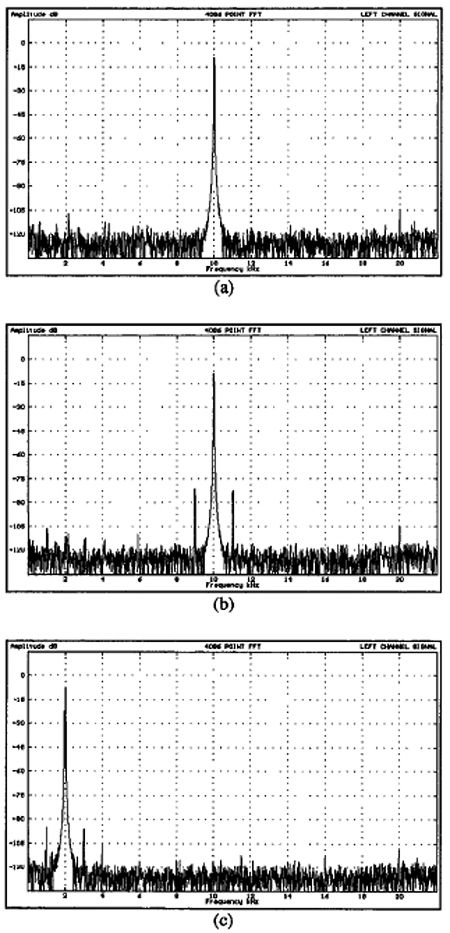
Fig.26 Musical Fidelity Digilog, 16-bit, 4x-oversampled 100% DAC: measured jitter error spectra for (from top to bottom): a) 10,001Hz at 0dBFS audio, no jitter; b) 10,001Hz at 0dBFS audio, 10ns peak 1kHz jitter; c) 2001Hz at 0dBFS audio, 10ns peak 1kHz jitter.
This jitter-injection method can also be used to assess the performance of the PLL filter employed in the interface receiver inside the DAC; if the jitter frequency is increased while maintaining constant amplitude, the amplitude of the error sidebands also remains constant until the break frequency of the loop is encountered. This technique was used to determine that the PLL cutoff frequency of the Musical Fidelity DAC was approximately 5kHz, implying that any jitter components below this frequency won't be attenuated by this particular unit, and will contribute to jitter error at the DAC.
Impulsive Sample DAC: We now progress to the impulsive DAC model, in which digital data samples are output as weighted impulses with no interaction between adjacent samples (fig.23b). The output impulses are infinitesimally narrow and occur at a sampling rate fs (44.1kHz in our simulations). Of course, this is a theoretical construct; no practical DAC would be able to create such an output pulse train. Nevertheless, the impulsive model fairly approximates a heavily oversampled PDM DAC (eg, Philips Bitstream) subject to a jitter process, where each 44.1kHz audio sample is represented by many discrete output pulses, each of unit amplitude and each subject to the same timing error. Referring to fig.23b, the continuous error signal en due to one audio sample An jittered by tjn can be written:
Equation 19:
![]()
where δ(t) corresponds to a Dirac impulse at time t.
Hence the discrete error spectra due to a sequence en is:
Equation 20:
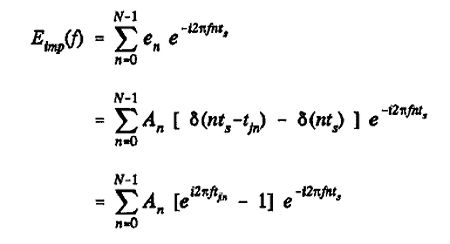
Now if we assume that the jitter interval tjn is very much less than the sampling interval ts, then:
Equation 21:

Thus, the error spectra are simply the Fourier transforms of the product sequence Antjn scaled to rise with frequency. Equation 21 can be compared to the error spectra obtained for the 100% DAC model (Equation 18); intermodulation between signal and jitter frequencies is still expected in the impulsive error spectra, but the intermodulation components will have different weights than those obtained from the 100% model.
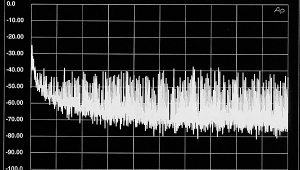
This is best illustrated by comparing error spectra for the two models when a 1kHz tone is jittered by wideband white noise (fig.27). The error spectra for the 100% model are essentially flat with frequency; the impulsive error rises with frequency at 6dB/octave (the exact frequency at which the two curves intersect depends upon the audio signal frequency and the statistical properties of the jitter noise).

Fig.27 Simulated 1/3-octave-smoothed error spectra for 1kHz, 0dBFS tone jittered by 10ns peak white noise; flat curve is 100% DAC model; upward-sloping curve is impulsive DAC model.
The accuracy of the impulsive DAC jitter error model can be confirmed by comparing simulated (fig.28a-c) and measured (fig.29a-c) results for the same signals used in "100% Sample DAC" (fig.26a-c). The measured results, made using a Meridian 203 Bitstream DAC, clearly show good agreement (within 2dB) with the simulations. The jitter injection interface was also employed to determine that the cutoff frequency of the Meridian PLL was higher than 10kHz.
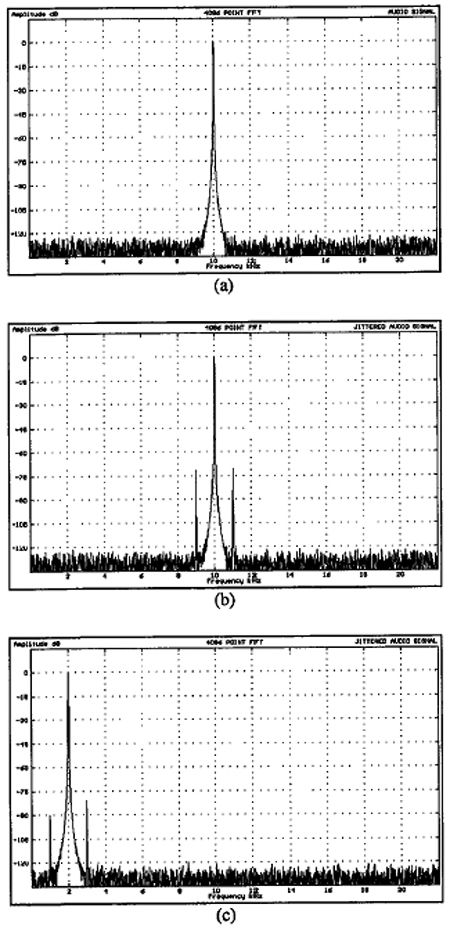
Fig.28 Simulated jitter error spectra for impulsive DAC model (from top to bottom): a) 10,001Hz at 0dBFS audio, no jitter; b) 10,001Hz at 0dBFS audio, 10ns peak 1kHz jitter; c) 2001Hz at 0dBFS audio, 10ns peak 1kHz jitter.

Fig.29 Meridian 203 Bitstream DAC: measured jitter error spectra for (from top to bottom): a) 10,001Hz at 0dBFS audio, no jitter; b) 10,001Hz at 0dBFS audio, 10ns peak 1kHz jitter; c) 2001Hz at 0dBFS audio, 10ns peak 1kHz jitter.
The same measurement made on another Bitstream D/A processor, the Audiolab 8000 DAC, reveals no jitter error at all (fig.30); this is due to the superb PLL performance of this model, offering a (claimed) closed-loop cutoff frequency of just 13Hz, where all audio-frequency interface jitter will be attenuated to inaudible levels. (Note that the noise seen at 400Hz in this diagram is due to a ground-loop problem in the test apparatus.)

Fig.30 Audiolab 8000 Bitstream DAC: measured jitter error spectra for 10,001Hz at 0dBFS audio, 10ns peak 1kHz jitter. Note the absence of error sidebands at 9kHz and 11kHz.
The greatest differences between 100% and impulsive DAC jitter errors occur when the signal frequency is low. Figs.31 & 32 show simulations and measurements, respectively, for a 0dBFS, 100Hz audio signal jittered by 10ns, 4kHz sinusoidal jitter. The jitter error is about 30dB higher in the impulsive (Bitstream) DAC. Thus, audible noise modulation can occur when impulsive DACs are jittered while reproducing low-frequency audio signals, and this may well be the reason some reports have suggested that Bitstream DACs lack "dynamics" and "rhythm and pace," (footnote 16) since most of the rhythmic content in music occurs at low frequencies and can be of high peak level.

Fig.31 Simulated jitter error spectra for 100.01Hz at 0dBFS, 10ns peak 4kHz jitter, for a) 100% DAC model (top) and b) impulsive model (bottom).

Fig.32 Measured jitter error spectra for 100.01Hz at 0dBFS, 10ns peak 4kHz jitter, for a) Musical Fidelity Digilog (top) and b) Meridian 203 (bottom).
Footnote 16: Martin Colloms, Hi-Fi News & Record Review, October 1989, pp.83-85.
- Log in or register to post comments