| Columns Retired Columns & Blogs |
In Search Of The Audio Abode---The Hi-fi House Page 2
For a 20dB noise level at the property line---the loudness of a whisper heard from 5'---your plot can be a more modest 40 acres in size. Are you starting to get the point? Unless you live on a country estate (or farm), open-window listening is just not very practical.
Footnote 1: Even when you have an optimally dimensioned room, successfully positioning two loudspeakers in a room is a large enough subject for a complete article. But as a rough rule, using the two loudspeakers to divide each room dimension into thirds excites low-frequency standing waves to the smallest extent and is therefore a good starting point. Quad's Peter Walker once told me that the best place to position a pair of loudspeakers was one-third of the way out into the room along each of the two diagonals, something confirmed by two software packages that I recently examined. The first is a service supplied by Snell dealers to owners of Snell loudspeakers free of charge. The customer supplies his room dimensions and the program indicates the best, good, and worst positions in the room. In Tom Norton's interview with Snell's Kevin Voecks last month, it was mentioned that non-Snell owners might also be able to use this service. Write to Snell Acoustics, 143 Essex Street, Haverhill, MA 01830, for further details.
Note that the preceding figures are theoretical, hence approximate. The calculations are pretty accurate for a point source radiating into an open space, but actual sound attenuation with distance can vary by as much as 10dB depending on the lay of the land, its ground cover, and the facing direction of your window(s). For example, if you're near a hilltop and your window faces your neighbor's window on the next hilltop, sound attenuation will be much less than calculated. If your neighbor's house is below yours on the same hill, and his windows face the same direction as yours (that is, away from the source of your noise), and there is a stand of trees between you, attenuation will be substantially greater---by as much as 15dB or so. But we're still talking large plots of real estate. The sensible alternative is to listen with your windows closed.
A single pane of glass bestows almost 25dB of sound attenuation, while a second pane will add about 20 more. Together, they will give you about as much noise reduction as 130' of outdoor distance, before your racket has even left the house. Then, a mere 34' of distance will attenuate outgoing and incoming noise by an additional 20dB, reducing your original 90dB to a neighbor's 25dB. That "impractical" 10dB background is easily achievable, with only 75' of distance, on a half-acre lot.
Closed-window listening is clearly the best solution to the privacy problem, for people who can't afford a rural estate.
Dimensional ratios:
In any enclosed space, soundwaves will bounce back and forth several times between opposite room boundaries before dying out. At most frequencies, the decay is rapid, but when a sound's wavelength is precisely twice that of a room dimension, something interesting happens: Compressions and rarefactions occur simultaneously at opposite boundary surfaces, reinforcing the wave from both directions and creating a resonant condition. This is called a standing wave, because the zones of compression and rarefaction in the room are stationary during the resonant period. (Of course, the soundwaves themselves aren't stationary: they are continually bouncing back and forth between opposite walls.) (fig.2)

Fig.2 A standing wave between two wall boundaries. The reflecting soundwaves reinforce one another at the boundaries and produce a pressure dip in the middle of the room. Both effects are minimized by placing the loudspeakers and the listening seat at intervals of 1/3 of their room dimension.
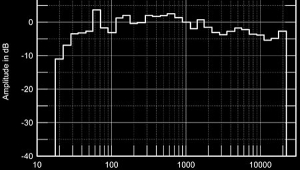
Like most other resonant conditions, standing waves produce a fundamental tone (the lowest-frequency resonance the space will support) and a series of harmonics at one-octave intervals. If the fundamental is at 20Hz, there will be other, progressively weaker ones at 40, 60, 80, 100, 120, 160Hz, and so on. Each of these harmonics causes a frequency-response peak in the room, with a dip midway between each adjacent pair. Fig.3A shows the effect on an otherwise flat response of the fundamental and first four harmonics of the 20Hz standing wave.
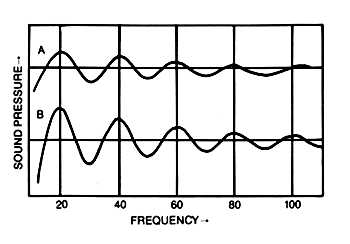
Fig.3: A (Above): The standing-wave resonances from a 20-Hz tone in a 27.5' room. B (below): The effect of two such resonances in a square room.
Because a rectangular room has three dimensions (length, width, and height), it will exhibit three sets of standing waves. And if any two sets of these occur at the same frequencies, they will reinforce one another and exacerbate the room's frequency-response irregularities (fig.3B). The worst case is when all three room dimensions are the same, at which time the lower-range resonances can become severe enough to cause pronounced hangover at those frequencies.
Since we can't get rid of the resonances (although some strategically placed ASC Tube Traps will help matters greatly), the next best thing is to stagger the resonant frequencies so that the response irregularities are as widely and as regularly spaced as possible. We do this by the proper choice of room dimensions (footnote 1).
Since we are working with three of these---length, width, and height---we have three frequencies to place within each octave. This means the intervals between them should, ideally, be 1/3rd-octaves. Thus, the second-largest room dimension should be 1.25 times the smallest, and the largest dimension should be 1.6 times the smallest. Fig.4 shows what this accomplishes.

Fig.4 (above): The standing-wave series for the dimensions of an ideally proportioned listening room. (below): The sound-pressure frequency response of a room having these dimensional ratios.
Most residences have 8' ceilings, so if we are to end up with the proper 1/3-octave standing-wave distribution, the width and length must be based on that 8' height. Here's what that gives us: For width, 8 x 1.25 = 10'. For length, 8 x 1.6 = 12.8'. A nice, compact little room---which, unfortunately, won't support deep bass worth a damn!
Size:
Here's another reason perfectionist audio can be very pricey: Low bass requires a large listening room, and you don't often find large rooms in $125,000 houses these days.
When a sound is pitched below the lowest standing-wave frequency in the room, compression waves traveling in one direction are partially canceled by rarefactions traveling in the opposite direction, diminishing the strength of both. This happens to some extent at all other frequencies except those involved in standing-wave activity, but when the room dimension is able to support several waves in a row, the cancellations are of short duration and occur randomly in different places in the room. When only a fraction of the wave can be accommodated, though, bass performance is seriously impaired throughout the entire room.
Footnote 1: Even when you have an optimally dimensioned room, successfully positioning two loudspeakers in a room is a large enough subject for a complete article. But as a rough rule, using the two loudspeakers to divide each room dimension into thirds excites low-frequency standing waves to the smallest extent and is therefore a good starting point. Quad's Peter Walker once told me that the best place to position a pair of loudspeakers was one-third of the way out into the room along each of the two diagonals, something confirmed by two software packages that I recently examined. The first is a service supplied by Snell dealers to owners of Snell loudspeakers free of charge. The customer supplies his room dimensions and the program indicates the best, good, and worst positions in the room. In Tom Norton's interview with Snell's Kevin Voecks last month, it was mentioned that non-Snell owners might also be able to use this service. Write to Snell Acoustics, 143 Essex Street, Haverhill, MA 01830, for further details.
The second piece of software, an update of his LMP program, was written by Ralph Gonzalez of Delaware Acoustics for Sitting Duck Software. The user enters one room dimension at a time and a plot shows how strongly each of the main standing-wave modes will be excited at each point along that dimension. You choose a speaker position where as many of the standing waves as possible are close to the 0dB line, then move on to the second room dimension. For more details on this useful program, write to Delaware Acoustics, P.O. Box 54, Newark, DE 19810.---JA
- Log in or register to post comments