Reference

These and other factors have been instrumental in improving CD's standing in audiophile affections, but few who have experienced hi-rez audio from 24/96 DVD-V, from DVD-Audio, or from SACD would assert that even pristine 16/44.1 audio comes close to being transparent. Fewer people have had the chance to hear 16/96 audio, but, as Pioneer's double-speed DAT players demonstrated more than a decade ago, increasing the sampling rate alone has a significant effect on sound quality. Ken Ishiwata told me many years ago that Marantz had experimented with sampling rates up to 500kHz, and that with every increase up to that rate, the sound quality improved.

In recent years the time-domain performance of anti-alias and reconstruction filters has increasingly been blamed for CD's residual failings, although in truth the idea is not new. Wadia first popularized the notion in 1988 with the introduction of its Digimaster upsampling algorithm, which deliberately sacrificed a flat top-octave frequency response in order to improve the reconstruction filter's time-domain performance. Five years later Ed Meitner took a different approach with the IDAT D/A converter, which incorporated two reconstruction filters and switched between them dynamically according to the nature of the signal. One filter, of the classic brick-wall variety, was used for relatively steady-state signal segments; the other, which sacrificed frequency-response accuracy for a shorter impulse response, took over when the signal became more transient in nature.

In fact, there are two distinct time-domain issues with digital filters, the first of which was highlighted as long ago as 1984, in an AES paper by Roger Lagadec (of Studer) and Tom Stockham (of Soundstream) (footnote 4). To paraphrase, what Lagadec and Stockham identified was the importance of the time-domain corollary of using digital filters with in-band ripple. Low-pass filters, both analog and digital, come in four basic forms. In the first, the passband (the frequency range to be passed unattenuated) and the stopband (the frequency range to be attenuated) are both monotonic, which means they are ripple-free. The Butterworth filter is an example. In the second form (eg, a Chebyshev type 1 filter), the passband has ripple but the stopband is monotonic. In the third form (eg, Chebyshev type 2), the passband is monotonic and the stopband has ripple. And in the fourth (eg, elliptical), both the passband and the stopband have ripple.

The digital filters used in oversampling A/D and D/A converters are usually of the last type, so they have ripple in the passband. If this ripple is considered simply in terms of the human ear's sensitivity to amplitude changes, then a passband ripple specification of, say, ±0.5dB might be just acceptable. But as Lagadec and Stockham pointed out, ripple in the passband indicates the presence of attenuated echoes in the time domain. In the case of a 48kHz sampling rate linear phase filter with 1024 cycles of ±0.5dB ripple in the passband, two echoes are present, each at –32dB and with a delay of approximately 40 milliseconds. Because the filter is phase linear, one of these echoes is a pre-echo and the other a post-echo; the former, in particular, gives rise to a clearly audible coloration.

Some, perhaps many, early digital filters suffered this problem. But the superior passband ripple of the digital filters used in modern A/D and D/A converters, which may be only ±0.0002dB or lower, has, to all intents and purposes, removed this problem. So I won't consider it further here.

The second time-domain effect has nothing to do with discrete echoes but relates to how the system impulse response becomes "smeared" in time as a result of low-pass filtering. If a narrow impulse—sufficiently narrow that it occupies only one sampling period—is recorded via an A/D converter, the result will typically look like fig.1. Although the input signal was only one sample wide, in the recorded version the impulse energy has been smeared over many samples due to the ringing behavior of the anti-alias filter. In most cases, as here, the filtering will be applied digitally within an oversampling converter and will be linear-phase. This removes the possibility of audible phase distortion but results in a symmetrical impulse response having a pre-response before the main peak. Such acausal (cause before effect) behavior is rare in nature and stands accused of imprinting digital audio with a characteristic, unnatural sound quality.

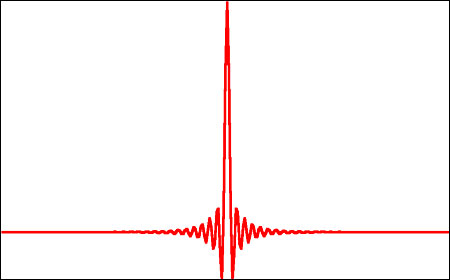
Fig.1 Typical impulse response of a linear-phase, brick-wall filter.

There are various ways this can be ameliorated. If the sampling rate is increased and the filter corner frequency raised in line with it, the impulse response will look the same but, because the sampling period is reduced, it will occupy a commensurately shorter time period. Even better, the increased bandwidth above 20kHz can be used as an extended transition band, permitting the use of a filter with a gentler onset. This will further reduce the length of the impulse response. If the sampling rate is immutable, then all that can be done is to juggle the relative amounts of pre- and post-response. By changing from a linear-phase to a minimum-phase filter, for instance, all pre-responses are removed, but now the filter will introduce potentially audible phase distortion.

The Experiment
As I've mentioned in passing in these pages before, I'm not entirely convinced by the argument that energy smear explains "digital sound." The theoretically ideal digital reconstruction filter—which is physically unrealizable but would produce an exact reconstruction of the sampled waveform—has what is called a sinc(t) impulse response that stretches from plus to minus infinity on the time axis and decays very slowly on either side of its central peak. This is the worst possible filter in terms of energy smear, yet it exactly reproduces the sampled waveform.

Hence the experiment I mentioned at the start of this piece, and its reprise here. If energy smear is a real, audible effect as claimed, then this experiment should prove it unequivocally. What I did was to create seven related digital filters based on a 28th-order Butterworth low-pass filter with a corner frequency of 21.3kHz, this being chosen to keep the passband response to 20kHz flat to 0.1dB. A Butterworth response was chosen not because it is representative of real-world anti-alias filters but because: a) it has a monotonic (ripple-free) passband response (so no echoes), and b) it makes the math easier. As the sidebar "How the Filters Were Designed" explains, choosing a classic analog filter characteristic with a known phase response allows the impulse response to be manipulated as desired. A 28th-order incarnation was chosen because this gives an impulse-response decay similar to that of brick-wall 44.1kHz anti-alias filters. Frequency and phase responses for this filter are shown in fig.2.

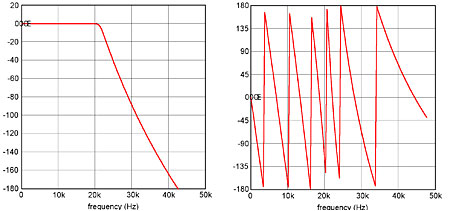
Fig.2 Frequency (left) and phase responses of the 28th-order Butterworth "donor" filter used for this experiment.

Manipulating this donor filter allowed the creation of the seven 96kHz digital filters, each with 256 coefficients, whose impulse, frequency, and phase responses are shown in fig.3. The first is a linear-phase filter with symmetrical impulse response and flat phase response (ie, no phase distortion). Note that its frequency response accurately mimics that of the Butterworth filter to below –130dB. The second filter is an interpolated phase filter with half the phase shift of the Butterworth. This reduces the amount of impulse pre-response. Note once more that the frequency response is accurate to below –130dB, and that the phase response goes haywire only above about 35kHz, at which point the response is already 140dB down. Filter 3 is minimum phase and so the digital equivalent of the donor Butterworth, as can be confirmed by comparing its frequency and phase responses with those of fig.2. In this case the impulse has no pre-response, only post-response. Filter 4 is a maximum-phase filter that has the same impulse response as the minimum-phase filter but reversed in time. This filter's impulse has only pre-response, no post-response. Filters 5, 6, and 7 are all-pass equivalents of Filters 2, 3, and 4—ie, they have the same phase response but a flat frequency response—and in energy-smear terms their impulse responses look particularly nasty.

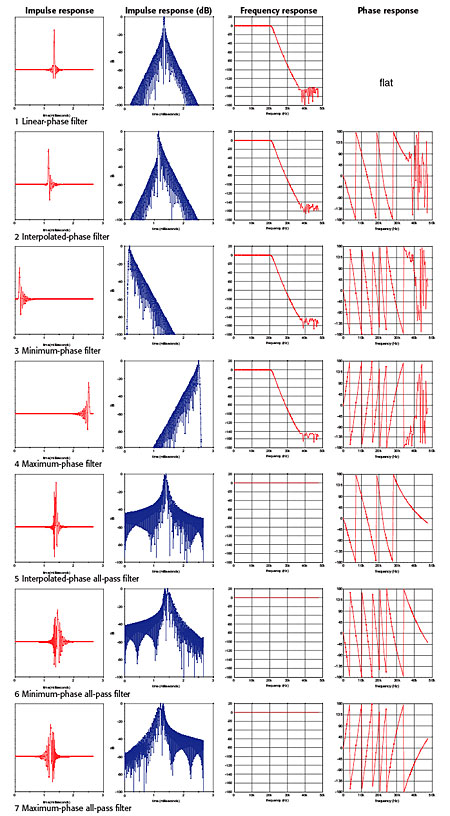
Fig.3 Impulse, frequency, and phase responses of the seven digital filters applied to the four music tracks listed in Table 1.

Table 1: Music Tracks Used For The Listening Tests

Group 1
"Desert Flower" Peppino D'Agostino: Acoustic Guitar AIX 80013
Group 2
Haydn: Piano Trio 2, Menuetto Pro Arte Trio AIX 1340AX
Group 3
"Now Is the Month of Maying" Zephyr: Voices Unbound AIX 80012
Group 4
"Mistreated but Undefeated Blues" Ray Brown Trio: Soular Energy Hi-Res HRM 2011

These seven filters were applied to the four 24/94 tracks listed in Table 1, which were recorded via S/PDIF from DVD-As. These tracks were chosen not just for their musical diversity but also because they have very different spectra, and will therefore be modified by the filtering in diverse ways. The original and filtered tracks were then burned to DVD-R for listening comparisons using Minnetonka's discWelder Chrome II (thanks to Minnetonka Software for upgrading my v1). To avoid any self-fulfilling prophecies, I eschewed listening duties myself and instead provided four copies of the disc to JA to distribute as he saw fit. The identities of the filters were unknown to the listeners, although they were presented in the same order for all four tracks to allow cross-referencing.

If energy smear is a real and significant effect, then these seven very different filters should have made obviously different imprints on the sound quality of the test tracks. But the listening results, described in the sidebar, indicate that the sonic disparities between the filtered tracks and the 24/96 originals were very difficult to pin down. Only Filter 4, the maximum-phase filter in which all the ringing is pre-ringing, introduced degradation that the listeners felt confident in identifying. It seems that energy smear, supposedly a bête noir of digital audio, seems surprisingly reluctant to show its face.

---

Footnote 4: R. Lagadec and T.G. Stockham, "Dispersive Models for A-to-D and D-to-A Conversion Systems," Preprint 2097, 75th Audio Engineering Society Convention (1984).