| Columns Retired Columns & Blogs |
Measuring Loudspeakers, Part Three Page 2
Second is the microphone mounting arrangement. The MLS technique is very sensitive to reflections of the sound emitted by the loudspeaker. It is important, therefore, to mount the microphone so that any reflections from the stand and its associated hardware occur after or at the same time as the inevitable reflections from the room boundaries. The B&K microphone is held endwise by a female XLR plug that is flush-mounted into a 2m length of ½" plumbing pipe. This pipe is held in a conventional microphone stand, but with the upright and clamp 1.5m away from the microphone capsule. Fig.23 shows the difference in the measured response of a BBC LS3/5A loudspeaker at a distance of 50" (1.27m) made by replacing this custom stand with a commercial boom stand and a conventional spring clamp. (The FFT window and time data length were identical for both measurements.) Ripples in the treble response averaging ±0.5dB in amplitude can be seen, these resulting from acoustic reflections from the stand and mounting hardware.
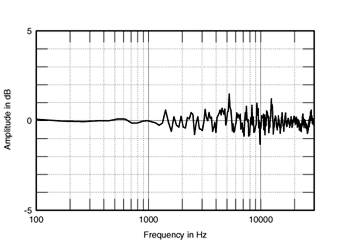
Fig.23 Difference in the measured response of a BBC LS3/5A loudspeaker at a distance of 50" made by replacing custom stand with a commercial boom stand and a conventional spring clamp.
The measurement system's antialiasing filter also introduces a small amount of response error. This too is subtracted from the calculated response for the graphs published in Stereophile. If you're not careful, you also get ripples in the measured response from the windowing used to remove room reflections. With a rectangular window, which gives the best frequency resolution, it is important to set the markers where you wish to truncate the impulse-response data at amplitude values as close as possible to zero. Otherwise the result will be ripples in the FFT-derived amplitude response. Tapered windows, where the farther away a datum point is from the center of the time window, the more it is attenuated, can also be used, but this is at the expense of frequency resolution [54].
It is typical Zen wisdom that the ideal room for measuring a loudspeaker using MLS techniques is an anechoic chamber. Not for quietness—the MLSSA system has good immunity to environmental noise, and I can measure loudspeakers in Stereophile's listening room, averaging up to 128 separate measurements to maximize S/N Ratio. However, remember that you have to window out room reflections in order to extract a loudspeaker's anechoic response. Truncating the time data in that manner will reduce both the plot's frequency resolution and the lowest frequency at which valid data will be produced. With a time window truncated to 5ms, for example, the response will only be accurate down to 200Hz. The farther away the room walls, or the more absorptive the room walls, the longer the time window that can be analyzed and the more accurate the measurement. Alternatively, the microphone can be placed farther away from the speaker for the same bandwidth and frequency definition.
In my room, I build an "acoustic black hole" on the floor between the speaker and the microphone stand using a 10" mat of several kinds of absorbent foam. This does a good job of absorbing floor reflections in the midrange and treble, meaning the main room reflection is now that from the ceiling. (This can be seen in a speaker's impulse response—fig.9, Stereophile, December 1998, p.79—as the small ripple near the right-hand side of the graph.)
Older engineers are probably used to measuring a speaker's frequency response at 1m. This, I feel, is too close for all but very small speakers (see later). I therefore use a standard microphone distance of 50" (1.27m), which is the farthest I can get back in my room and still preserve reasonable measurement bandwidth. Ideally, I would like to measure at 2m, where a large loudspeaker's drive-units will be better-integrated and where there will be less proximity effect (more on this later).
There is a problem with taking the response at just one point in that there is almost too much information. Some of the fine detail will be specific to just that one point in space. With a loudspeaker whose drive-units are mounted in some kind of vertical array, it seemed sensible to implement some kind of spatial averaging. This would smooth out any position-dependent wrinkles in the measured response, while leaving the significant information intact. Accordingly, my published responses are the average of seven measured responses, taken at 5 degree intervals across a 30 degrees horizontal window on the reference axis.
- Log in or register to post comments