| Columns Retired Columns & Blogs |
Measuring Loudspeakers, Part One Page 4
In 1990 Ronald Aarts of Philips [9] carried out a study of the effect of loudspeaker response on perceived loudness. He concluded that weighting the spectral balance with the popular noise A-weighting curve gave limited correlation with subjective loudness, instead calculating the loudness in phons based on critical-band analysis (ISO932B). Critical-band analyzers not being easy to come by, at Stereophile, I feed the loudspeaker with 20kHz-bandwidth noise at a standard level, capture the output waveform with the DRA Labs MLSSA system used in its storage-oscilloscope mode [10], and apply B-weighting to the 1/10-octave-smoothed power response to reduce the effect of bandwidth differences. Stereophile has performed four sets of single-blind tests involving 30 different loudspeaker models with the loudnesses equalized on the basis of the B-weighted sensitivity assessed in this manner [11, 12, 13, 14]. These tests indicate a reasonable connection with perceived loudness on music. Only with loudspeakers that had a grossly unflat on-axis response did it still prove somewhat unreliable. Analysis of the archived data using an ISO932B figure is a future project.
What is a typical loudspeaker sensitivity? Fig.1 tabulates the calculated B-weighted sensitivities for 261 of the loudspeakers reviewed in Stereophile between January 1991 and June 1997. The mean measured sensitivity is 88dB(B)/2.83V/m; the median is 85dB(B). Almost 40% of the models measured had B-weighted sensitivities falling between 84.5dB and 87.4dB. The distribution seems roughly "Normal," with only a few models falling below 80dB(B) or above 90dB(B). The low-sensitivity models tend to be panel speakers of various kinds, while all the speakers of 95dB(B) sensitivity or higher are professional monitors (and one musical instrument speaker measured for curiosity's sake).
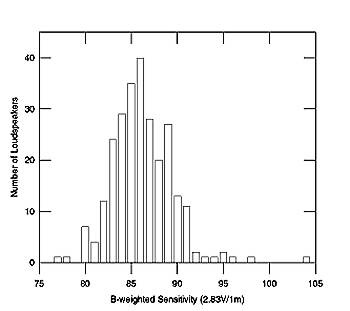
Fig.1 261 loudspeakers, B-weighted voltage sensitivities.
The relatively narrow spread of sensitivities should not come as a surprise. To achieve a high sensitivity requires heroic engineering, which will always be expensive. All speaker designers are constrained by budget constraints, which in turn mean that they will tend to settle on similar compromises involving magnet size, voice-coil design, and cone area.
In general, my measured sensitivities are slightly low compared with those published by the speakers' manufacturers. Mostly, I believe this is due to the optimistic nature of published sensitivity specifications. But it does need to be pointed out that Stereophile's office is located in Santa Fe, New Mexico at an altitude of 2150m (7000'). A series of experiments, measuring the same loudspeaker samples in Santa Fe and at sea level [15, 16, 17], showed that the only substantial effect on loudspeaker performance due to the altitude was a reduction in sensitivity. Rather than measure sensitivity directly, therefore, I compare each speaker's spl with that produced by a reference speaker (a BBC LS3/5A) that I have measured both at altitude and at sea level. It is possible, therefore, for a systematic error to have crept into my measurements. However, I don't believe this to be more than ±1dB.
Electrical Impedance
If the amplifier that drives a loudspeaker behaves as a voltage source, the loudspeaker's impedance will indicate how much current it will suck from that amplifier. Impedance is both reactive (ie, it has a nonzero electrical phase angle) and varies with frequency [18].
It can be measured in two ways. First is to measure the electrical impulse response of a voltage divider formed by the loudspeaker and a standard resistor and calculate the transfer function by performing a Fast (Discrete) Fourier Transform on the time-domain data [19]. Second is to use a swept sinewave signal or a series of discrete-frequency sinewaves to drive the loudspeaker-under-test, keeping the current constant and measuring the magnitude and phase independently [20]. In practice, the constant-current source is replaced by a constant-voltage source and a series high-value resistor, which means that error creeps in for high-value impedance maxima [21].
- Log in or register to post comments