| Columns Retired Columns & Blogs |
Listening #90 Page 3
Inspired by fig.2 on p.54 of "Arc Angles"—it portrays the record center, tonearm pivot center, and stylus location as three points of a triangle, and models that triangle in two different ways, using two different zero-error radii, and is reprinted here as fig.1—I set about plotting the Schick arm's known dimensions, intending to use the law of cosines (footnote 1) to see if Keith's nulls could possibly work with this arm. Of course, I knew the size of only one angle: 72.89 degrees (°), which I arrived at by subtracting the Schick's specified 17.11° offset from 90°. But because the law of cosines can be used in this way only when the known angle is included between two known sides, I had to approach this on a trial-and-error basis, punching in various radii to see how close each came to the Schick's preferred mounting distance of 304.75mm.
Footnote 1: That makes me sound smarter than I am: A quick search of the Internet is all you need to turn up a cosine-rule calculator such as the one I found here.
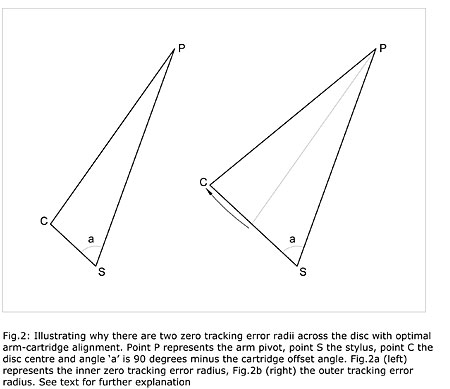
Fig.1 Illustrating why there are two zero tracking-error radii across the disc with optimal arm-cartridge alignment. Point P represents the arm pivot, point S the stylus, point C the disc centre and angle "a" is 90° minus the cartridge offset angle. Fig.1a (left) represents the inner zero tracking error radius, Fig.1b (right) the outer tracking error radius. (From "Arc Angles," Stereophile March 2010, p.51).
It turned out, somewhat disappointingly, that Keith's 61.6mm and 118.4 radii produced two different spindle-to-pivot dimensions, suggesting that Schick's offset and Keith's radii are incompatible, howsoever slightly. (The difference between the two spindle-to-pivot dimensions was "only" 0.67mm.)
I wanted to know the best way around that hurdle, so I called Keith Howard and explained my dilemma. He said that I should enter the Schick's effective length into his ArmGeometer freeware (footnote 2), in order to calculate the ideal overhang and offset angle for such an arm, and note whether the latter is greater or smaller than the Schick's actual offset. The reason for doing so: As Howard has discovered, there is a complementary relationship between overhang, in millimeters, and offset, in degrees. Thus, given a situation in which an arm's fixed offset angle is too great by x number of degrees, one can compensate for the discrepancy by adding that same number—in millimeters—to the ideal overhang (footnote 3). For the 317.57mm-long Schick, ArmGeometer recommends an overhang of 11.69mm and an offset of 16.46°. Since the Schick's 17.11° offset exceeds the ideal by 0.65, the user must add 0.65mm to the overhang. All that remains is to subtract the new overhang dimension—12.34mm—from the effective length, for a new spindle-to-pivot distance of 305.23mm. That's your new mounting dimension, boys: Drill carefully!
We're halfway there. We've determined, mathematically, that the Schick arm can be aligned acceptably well. But because in doing so we cheated a bit and moved two of our elements, howsoever proportionately, we must now go back to the ArmGeometer and relocate those zero-error radii. And we'll do that sneakily, using the software's graphing function (Item 3 on the ArmGeometer menu), which calculates and displays a distortion curve for our arm in its new location/overhang, compared with the curve for a perfectly aligned arm (ie, one in which offset angle really can be adjusted) with the same effective length. Looking at the Schick's curve, Keith and I noted zero distortion at the radii of 61.1mm and 125.7mm. Those numbers are acceptable, partly because 61.1mm remains close to the innermost modulated groove, and partly because the maximum distortion is, at most, only one or two tenths of a percent greater. Done!
The DB Systems DBP-10 protractor
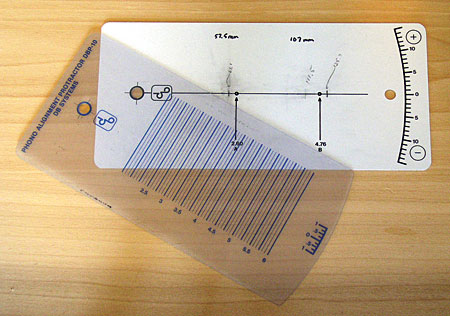
With careful attention to sizing and given a good, crisp printer, Keith Howard's software can be used to create a protractor based on those or any other pair of zero-error radii. But I'm lucky to have a DB Systems DBP-10 protractor, which can be used to gauge alignment accuracy at any point or points between 44 and 153mm from the spindle. I simply used a sharp pencil and a stainless-steel ruler to mark the extra radii on my protractor's scale, after which it was easy to confirm perfect tangency with the DBP-10's translucent grid overlay. Not having tried every alignment tool on the market, I can't declare this or any other "the best"—but the DBP-10 is still my favorite, by far. And at just $49 plus postage, it's a hell of a bargain.
Final Thoughts
By the way, at one point while I was working in ArmGeometer, I entered all of the Schick tonearm's specified dimensions and came up with the radii 66.0 and 120.9mm—precisely the dimensions recommended on that tonearm's website. Notwithstanding my acceptance of the newer null values, it's clear that Herr Schick knows his math and, in the context of accepted alignment wisdom, has engineered his tonearm exquisitely well.
Before I leave this subject, I want to correct a statement I made in my March column, where I suggested that a mounting dimension other than the one recommended on Schick's website was needed to achieve (again, traditionally accepted) good alignment. I made that observation while under the lingering influence of a phono-alignment enthusiast who, some years ago, supplied me with a clear plastic ruler that he had drilled for a 7mm record spindle, and which he intended for use as a tonearm-mounting aid. I assumed that the spindle hole had been drilled accurately. It turns out not to have been—and now that I've bought a shiny new stainless-steel ruler, I've consigned the older tool to the bin where it belongs. I'm sorry if my sloppiness reflected poorly on Thomas Schick, whose wisdom and engineering skill I admire.
I was about to say something along the lines of "Don't get carried away," until I remembered the time and effort I've put into this myself: Looking up trig sites, marking new crosshairs on my protractor . . . even going to RadioShack for batteries for my digital caliper! Nevertheless, try to avoid stressing out. Set a time limit for yourself. Do your best, but no more. And don't even think about off-center records.
And finally: What about those minimum and maximum radii for modulated LP grooves? Keith Howard addressed that matter in "Arc Angles" and concluded, on the basis of his own record collection, that the safest thing is to accept 56mm and 146.3mm as the correct respective numbers.
That outer limit is beyond question, but 56mm for the inner limit? Hmmm†.†.†.
Measuring my entire collection of LPs, or even a sample large enough to be considered representative, is out of the question for now. Instead, I pulled from the shelves as many records as I could measure in half an hour (with the new ruler!), some chosen on the basis of presumably long recording durations, others grabbed at random. Here are the bottom 12, in descending order:
Moby Grape, Moby Grape (Columbia): 64mm
John Lennon, Plastic Ono Band (Mobile Fidelity Sound Lab): 64mm
J.S. Bach, Goldberg Variations, Landowska (RCA): 62mm
Britten, Rejoice in the Lamb (Argo): 62mm
Mahler, Symphony 2, Bernstein/NYP (Columbia): 62mm
Beethoven, Symphony 9, Munch/BSO (RCA): 61mm
Bill Monroe, Classic Bluegrass Recordings, Vol.1 (RCA): 61mm
The Kinks, The Kink Kronikles (Reprise): 60mm
The Replacements, Tim (Sire): 59mm
Elvis Costello and the Attractions, Get Happy!! (Columbia): 58mm
Procol Harum, Grand Hotel (Chrysalis): 58mm
Donovan: Barabajagal (Epic): 57mm
There were lots of surprises, of course, not least of which was the fact that Jascha Horenstein's brilliant recording of Mahler's Symphony 3 didn't come close. But hey: Barabajagal? Who saw that coming?
But there you have it. If I can spend 30 minutes measuring LPs pulled at random and come up with even one that's modulated all the way to 57mm, then a 56mm record is hardly impossible.
Footnote 1: That makes me sound smarter than I am: A quick search of the Internet is all you need to turn up a cosine-rule calculator such as the one I found here.
Footnote 2: www.audiosignal.co.uk/freeware.html.
Footnote 3: Where overhang and offset are both excessive, decreasing one also works to fix the other. Only in situations where one dimension is too great and the other too small is the user SOL.
- Log in or register to post comments




































